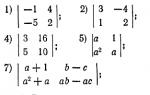Rješavanje sistema jednačina drugog reda. Sistem jednačina. Detaljna teorija s primjerima (2019). Rješavanje sistema jednačina

Neka je data kvadratna tabela od četiri broja a 1, a 2, b 1, b 2:

Broj a 1 b 2 - a 2 b 1 naziva se determinanta drugog reda koja odgovara tabeli (1). Ova determinanta je označena simbolom, tako da imamo:

Brojevi a 1, a 2, b 1, b 2 nazivaju se elementi determinante. Kažu da elementi a 1, b 2 leže na glavnoj dijagonali determinante, a 2, b 1 - na bočnoj dijagonali. Dakle, determinanta drugog reda jednaka je razlici između proizvoda elemenata koji leže na glavnoj i sekundarnoj dijagonali. Na primjer,

Razmotrimo sistem od dvije jednačine

sa dvije nepoznate x, y. (Pretpostavljamo da su koeficijenti a 1, b 1, a 2, b 2 i slobodni termini hXi h2 podaci.) Hajde da uvedemo notaciju.

Determinanta Δ, sastavljena od koeficijenata za nepoznate sistema (3), naziva se determinanta ovog sistema. Determinanta Δ x se dobija zamjenom elemenata prvog stupca determinante Δ slobodnim članovima sistema (3); determinanta Δ y se dobija iz determinante Δ zamjenom elemenata njenog drugog stupca slobodnim članovima sistema (3).

Ako je Δ ≠ 0, onda sistem (3) ima jedinstveno rješenje; određuje se formulama

x = Δ x /Δ , y = Δ y /Δ (5)

Ako je Δ = 0 i barem jedna od determinanti Δ x, Δ y je različita od nule, tada sistem (3) uopće nema rješenja (kako kažu, jednačine ovog sistema su nekompatibilne).

Ako je Δ = 0, ali i Δ x = Δ y = 0, onda sistem (3) ima beskonačno mnogo rješenja (u ovom slučaju jedna od jednačina sistema je posljedica druge).

Neka su u jednadžbi sistema (3)h 1 = h 2 = 0; tada će sistem (3) izgledati ovako:

a 1 x + b 1 y = 0, a 2 x + b 2 y = 0. (6)

Sistem jednačina oblika (6) naziva se homogenim; uvijek ima nulto rješenje: x = 0, y = 0. Ako je Δ ≠ O, onda je ovo rješenje jedinstveno, ali ako je Δ = 0, onda sistem (6), pored nulte jedinice, ima beskonačno mnogo drugih rješenja .

1204. Izračunaj determinante:

1205. Riješi jednačine:

1206. Riješite nejednačine:

1207. Pronađite sva rješenja za svaki od sljedećih sistema jednačina:

1208. Odredi pri kojim vrednostima a i b sistem jednačina 3x - ay = 1, 6x + 4y = b 1) ima jedinstveno rešenje; 2) nema rješenja; 3) ima beskonačno mnogo rješenja.

1209. Odrediti pri kojoj vrijednosti a sistem homogenih jednačina 13x + 2y = 0, 5x + ay = 0 ima rješenje različito od nule.

Rješavanje sistema linearnih algebarskih jednačina (SLAE) je nesumnjivo najvažnija tema u kursu linearne algebre. Ogroman broj problema iz svih grana matematike svodi se na rješavanje sistema linearnih jednačina. Ovi faktori objašnjavaju razlog za ovaj članak. Materijal članka je odabran i strukturiran tako da uz njegovu pomoć možete

• odabrati optimalnu metodu za rješavanje vašeg sistema linearnih algebarskih jednadžbi,
• proučavati teoriju odabrane metode,
• riješite svoj sistem linearnih jednačina razmatrajući detaljna rješenja tipičnih primjera i problema.

Kratak opis materijala članka.

Prvo dajemo sve potrebne definicije, koncepte i uvodimo oznake.

Zatim ćemo razmotriti metode rješavanja sistema linearnih algebarskih jednadžbi u kojima je broj jednačina jednak broju nepoznatih varijabli i koje imaju jedinstveno rješenje. Prvo ćemo se fokusirati na Cramerovu metodu, drugo, pokazaćemo matričnu metodu za rješavanje ovakvih sistema jednadžbi, i treće, analizirat ćemo Gaussovu metodu (metoda sekvencijalne eliminacije nepoznatih varijabli). Da bismo konsolidirali teoriju, svakako ćemo riješiti nekoliko SLAE na različite načine.

Nakon toga prelazimo na rješavanje sistema linearnih algebarskih jednadžbi opšteg oblika, u kojima se broj jednačina ne poklapa sa brojem nepoznatih varijabli ili je glavna matrica sistema singularna. Formulirajmo Kronecker-Capelli teorem, koji nam omogućava da uspostavimo kompatibilnost SLAE. Analizirajmo rješenja sistema (ako su kompatibilni) koristeći koncept baznog minora matrice. Također ćemo razmotriti Gaussovu metodu i detaljno opisati rješenja primjera.

Svakako ćemo se zadržati na strukturi opšteg rješenja homogenih i nehomogenih sistema linearnih algebarskih jednačina. Hajde da damo koncept fundamentalnog sistema rešenja i pokažemo kako se opšte rešenje SLAE piše pomoću vektora fundamentalnog sistema rešenja. Za bolje razumijevanje, pogledajmo nekoliko primjera.

U zaključku ćemo razmotriti sisteme jednačina koji se mogu svesti na linearne, kao i različite probleme u čijem rješavanju nastaju SLAE.

Navigacija po stranici.

Definicije, koncepti, oznake.

Razmotrićemo sisteme p linearnih algebarskih jednadžbi sa n nepoznatih varijabli (p može biti jednako n) oblika

Nepoznate varijable, - koeficijenti (neki realni ili kompleksni brojevi), - slobodni termini (takođe realni ili kompleksni brojevi).

Ovaj oblik snimanja SLAE se zove koordinata.

IN matrični oblik pisanje ovog sistema jednačina ima oblik,
Gdje - glavna matrica sistema, - matrica kolona nepoznatih varijabli, - matrica kolona slobodnih termina.

Ako matrici A dodamo matricu-stupac slobodnih pojmova kao (n+1)-ti stupac, dobijamo tzv. proširena matrica sistemi linearnih jednačina. Obično se proširena matrica označava slovom T, a stupac slobodnih pojmova odvojen je okomitom linijom od preostalih stupaca, tj.

Rješavanje sistema linearnih algebarskih jednačina naziva skup vrijednosti nepoznatih varijabli koji pretvara sve jednadžbe sistema u identitete. Matrična jednadžba za date vrijednosti nepoznatih varijabli također postaje identitet.

Ako sistem jednačina ima barem jedno rješenje, onda se zove joint.

Ako sistem jednačina nema rješenja, onda se zove non-joint.

Ako SLAE ima jedinstveno rješenje, onda se ono zove siguran; ako postoji više od jednog rješenja, tada – neizvjesno.

Ako su slobodni članovi svih jednačina sistema jednaki nuli , tada se sistem poziva homogena, inače - heterogena.

Rješavanje elementarnih sistema linearnih algebarskih jednačina.

Ako je broj jednačina sistema jednak broju nepoznatih varijabli i determinanta njegove glavne matrice nije jednaka nuli, tada će se takve SLAE zvati osnovno. Takvi sistemi jednačina imaju jedinstveno rješenje, au slučaju homogenog sistema sve nepoznate varijable su jednake nuli.

Počeli smo da proučavamo takve SLAE u srednjoj školi. Prilikom njihovog rješavanja, uzeli smo jednu jednačinu, izrazili jednu nepoznatu varijablu u terminima drugih i zamijenili je u preostale jednačine, zatim uzeli sljedeću jednačinu, izrazili sljedeću nepoznatu varijablu i zamijenili je u druge jednačine i tako dalje. Ili su koristili metodu sabiranja, odnosno dodali su dvije ili više jednadžbi kako bi eliminirali neke nepoznate varijable. Nećemo se detaljnije zadržavati na ovim metodama, jer su one u suštini modifikacije Gaussove metode.

Glavne metode za rješavanje elementarnih sistema linearnih jednačina su Cramerova metoda, matrična metoda i Gaussova metoda. Hajde da ih sredimo.

Rješavanje sistema linearnih jednadžbi Cramerovom metodom.

Pretpostavimo da treba da rešimo sistem linearnih algebarskih jednačina

u kojoj je broj jednačina jednak broju nepoznatih varijabli, a determinanta glavne matrice sistema je različita od nule, tj.

Neka je determinanta glavne matrice sistema, i - determinante matrica koje se dobijaju iz A zamenom 1., 2., …, n-ti kolonu odnosno kolonu slobodnih članova:

Uz ovu notaciju, nepoznate varijable se izračunavaju korištenjem formula Cramerove metode kao . Ovako se pronalazi rješenje sistema linearnih algebarskih jednačina korištenjem Cramerove metode.

Primjer.

Cramerova metoda .

Rješenje.

Glavna matrica sistema ima oblik . Izračunajmo njegovu determinantu (ako je potrebno, pogledajte članak):

Pošto je determinanta glavne matrice sistema različita od nule, sistem ima jedinstveno rešenje koje se može naći Cramerovom metodom.

Sastavimo i izračunajmo potrebne determinante (determinantu dobijamo tako što prvi stupac u matrici A zamijenimo stupcem slobodnih pojmova, determinantu zamjenom drugog stupca stupcem slobodnih pojmova i zamjenom treće kolone matrice A stupcem slobodnih pojmova) :

Pronalaženje nepoznatih varijabli pomoću formula :

odgovor:

Glavni nedostatak Cramerove metode (ako se to može nazvati nedostatkom) je složenost izračunavanja determinanti kada je broj jednačina u sistemu veći od tri.

Rješavanje sistema linearnih algebarskih jednadžbi matričnom metodom (pomoću inverzne matrice).

Neka je sistem linearnih algebarskih jednadžbi zadan u matričnom obliku, pri čemu matrica A ima dimenziju n sa n i njena determinanta je različita od nule.

Pošto je matrica A invertibilna, odnosno postoji inverzna matrica. Ako obje strane jednakosti pomnožimo lijevom, dobićemo formulu za pronalaženje matrice-stupca nepoznatih varijabli. Ovako smo matričnom metodom dobili rješenje za sistem linearnih algebarskih jednadžbi.

Primjer.

Riješiti sistem linearnih jednačina matrična metoda.

Rješenje.

Prepišimo sistem jednačina u matričnom obliku:

Jer

tada se SLAE može riješiti korištenjem matrične metode. Koristeći inverznu matricu, rješenje ovog sistema se može naći kao .

Konstruirajmo inverznu matricu koristeći matricu od algebarskih sabiranja elemenata matrice A (ako je potrebno, pogledajte članak):

Ostaje izračunati matricu nepoznatih varijabli množenjem inverzne matrice na matricu-kolona slobodnih članova (ako je potrebno, pogledajte članak):

odgovor:

ili u drugoj notaciji x 1 = 4, x 2 = 0, x 3 = -1.

Glavni problem pri pronalaženju rješenja sistema linearnih algebarskih jednadžbi metodom matrice je složenost pronalaženja inverzne matrice, posebno za kvadratne matrice reda većeg od trećeg.

Rješavanje sistema linearnih jednadžbi Gaussovom metodom.

Pretpostavimo da treba da nađemo rešenje za sistem od n linearnih jednačina sa n nepoznatih varijabli
determinanta glavne matrice koja je različita od nule.

Suština Gaussove metode sastoji se od sekvencijalnog eliminisanja nepoznatih varijabli: prvo, x 1 se isključuje iz svih jednačina sistema, počevši od druge, zatim se x 2 isključuje iz svih jednačina, počevši od treće, i tako dalje, sve dok ne ostane samo nepoznata varijabla x n u poslednjoj jednačini. Ovaj proces transformacije sistemskih jednačina da bi se sekvencijalno eliminisale nepoznate varijable naziva se direktna Gausova metoda. Nakon završetka naprednog poteza Gaussove metode, x n se nalazi iz posljednje jednačine, koristeći ovu vrijednost iz pretposljednje jednačine, izračunava se x n-1, i tako dalje, x 1 se nalazi iz prve jednačine. Proces izračunavanja nepoznatih varijabli pri prelasku sa zadnje jednadžbe sistema na prvu naziva se inverzno od Gausove metode.

Hajde da ukratko opišemo algoritam za eliminaciju nepoznatih varijabli.

Pretpostavit ćemo da , budući da to uvijek možemo postići preuređivanjem jednačina sistema. Hajde da eliminišemo nepoznatu promenljivu x 1 iz svih jednačina sistema, počevši od druge. Da bismo to učinili, drugoj jednačini sistema dodajemo prvu, pomnoženu sa , trećoj jednačini dodajemo prvu, pomnoženu sa , i tako dalje, na n-tu jednačinu dodajemo prvu, pomnoženu sa . Sistem jednačina nakon takvih transformacija će poprimiti oblik

gdje i .

Do istog rezultata bismo došli da smo izrazili x 1 u terminima drugih nepoznatih varijabli u prvoj jednačini sistema i zamenili rezultujući izraz u sve ostale jednačine. Dakle, varijabla x 1 je isključena iz svih jednačina, počevši od druge.

Zatim nastavljamo na sličan način, ali samo s dijelom rezultirajućeg sistema koji je označen na slici

Da bismo to učinili, trećoj jednačini sistema dodajemo drugu, pomnoženu sa , četvrtoj jednačini dodamo drugu, pomnoženu sa , i tako dalje, na n-tu jednačinu dodamo drugu, pomnoženu sa . Sistem jednačina nakon takvih transformacija će poprimiti oblik

gdje i . Dakle, varijabla x 2 je isključena iz svih jednačina, počevši od treće.

Zatim prelazimo na eliminaciju nepoznatog x 3, dok slično postupamo sa dijelom sistema označenim na slici

Tako nastavljamo direktnu progresiju Gausove metode sve dok sistem ne poprimi oblik

Od ovog trenutka počinjemo obrnuto od Gaussove metode: izračunavamo x n iz posljednje jednačine kao , koristeći dobivenu vrijednost x n nalazimo x n-1 iz pretposljednje jednačine, i tako dalje, nalazimo x 1 iz prve jednačine .

Primjer.

Riješiti sistem linearnih jednačina Gaussova metoda.

Rješenje.

Isključimo nepoznatu varijablu x 1 iz druge i treće jednačine sistema. Da bismo to učinili, na obje strane druge i treće jednačine dodajemo odgovarajuće dijelove prve jednačine, pomnožene sa i sa:

Sada eliminiramo x 2 iz treće jednadžbe dodavanjem lijevoj i desnoj strani druge jednadžbe lijevu i desnu stranu druge jednačine, pomnožene sa:

Ovim se završava potez naprijed Gaussove metode; počinjemo obrnuti potez.

Iz posljednje jednačine rezultirajućeg sistema jednačina nalazimo x 3:

Iz druge jednačine dobijamo .

Iz prve jednadžbe nalazimo preostalu nepoznatu varijablu i time dovršavamo obrnuto Gaussovom metodom.

odgovor:

X 1 = 4, x 2 = 0, x 3 = -1.

Rješavanje sistema linearnih algebarskih jednačina opšteg oblika.

Općenito, broj jednačina sistema p ne poklapa se sa brojem nepoznatih varijabli n:

Takvi SLAE možda nemaju rješenja, imaju jedno rješenje ili imaju beskonačno mnogo rješenja. Ova izjava se takođe odnosi na sisteme jednačina čija je glavna matrica kvadratna i singularna.

Kronecker–Capelli teorem.

Prije pronalaženja rješenja za sistem linearnih jednačina, potrebno je utvrditi njegovu kompatibilnost. Odgovor na pitanje kada je SLAE kompatibilan, a kada nekonzistentan daje Kronecker–Capelli teorem:
Da bi sistem p jednačina sa n nepoznatih (p može biti jednako n) bio konzistentan, potrebno je i dovoljno da rang glavne matrice sistema bude jednak rangu proširene matrice, tj. , Rang(A)=Rank(T).

Razmotrimo, kao primjer, primjenu Kronecker–Capellijeve teoreme za određivanje kompatibilnosti sistema linearnih jednačina.

Primjer.

Saznajte da li sistem linearnih jednačina ima rješenja.

Rješenje.

. Koristimo se metodom graničenja maloljetnika. Minor drugog reda različito od nule. Pogledajmo maloljetnike trećeg reda koji ga graniče:

Pošto su svi granični minori trećeg reda jednaki nuli, rang glavne matrice je jednak dva.

Zauzvrat, rang proširene matrice je jednako tri, pošto je umanjilac trećeg reda

različito od nule.

dakle, Rang(A), dakle, koristeći Kronecker–Capelli teorem, možemo zaključiti da je originalni sistem linearnih jednačina nekonzistentan.

odgovor:

Sistem nema rješenja.

Dakle, naučili smo utvrditi nekonzistentnost sistema koristeći Kronecker-Capelli teorem.

Ali kako pronaći rješenje za SLAE ako je uspostavljena njegova kompatibilnost?

Da bismo to učinili, potreban nam je koncept baznog mola matrice i teorema o rangu matrice.

Zove se minor najvišeg reda matrice A, različit od nule osnovni.

Iz definicije baznog minora slijedi da je njegov red jednak rangu matrice. Za nenultu matricu A može postojati nekoliko baznih minora; uvijek postoji jedan bazni minor.

Na primjer, razmotrite matricu .

Svi minori trećeg reda ove matrice jednaki su nuli, jer su elementi trećeg reda ove matrice zbir odgovarajućih elemenata prvog i drugog reda.

Sljedeći minori drugog reda su osnovni, jer su različiti od nule

Maloljetnici nisu osnovne, jer su jednake nuli.

Teorema o rangu matrice.

Ako je rang matrice reda p po n jednak r, tada se svi elementi reda (i stupca) matrice koji ne čine odabrani bazni minor linearno izražavaju u terminima odgovarajućih elemenata reda (i stupca) koji formiraju osnovni minor.

Šta nam govori teorema o rangu matrice?

Ako smo, prema Kronecker–Capellijevoj teoremi, uspostavili kompatibilnost sistema, tada biramo bilo koji bazni minor glavne matrice sistema (njen red je jednak r) i isključujemo iz sistema sve jednačine koje čine ne čine odabrani bazni mol. Ovako dobijena SLAE bit će ekvivalentna originalnoj, budući da su odbačene jednadžbe i dalje suvišne (prema teoremi o rangu matrice, one su linearna kombinacija preostalih jednačina).

Kao rezultat, nakon odbacivanja nepotrebnih jednačina sistema moguća su dva slučaja.

Ako je broj jednačina r u rezultirajućem sistemu jednak broju nepoznatih varijabli, onda će ona biti definitivna i jedino rješenje se može naći Cramerovom metodom, matričnom metodom ili Gaussovom metodom.

Primjer.

.

Rješenje.

Rang glavne matrice sistema je jednako dva, pošto je minor drugog reda različito od nule. Prošireni matrični rang je takođe jednako dva, pošto je jedini minor trećeg reda nula

a gore razmatrani minor drugog reda je različit od nule. Na osnovu Kronecker–Capelli teoreme, možemo tvrditi kompatibilnost originalnog sistema linearnih jednačina, budući da je Rank(A)=Rank(T)=2.

Kao base minor uzimamo . Formira se koeficijentima prve i druge jednačine:


Treća jednačina sistema ne učestvuje u formiranju baznog minora, pa je isključujemo iz sistema na osnovu teoreme o rangu matrice:


Tako smo dobili elementarni sistem linearnih algebarskih jednačina. Rešimo ga Cramerovom metodom:


odgovor:

x 1 = 1, x 2 = 2.

Ako je broj jednačina r u rezultirajućem SLAE manji od broja nepoznatih varijabli n, tada na lijevoj strani jednadžbe ostavljamo članove koji čine bazni minor, a preostale članove prenosimo na desne strane jednačine sistema sa suprotnim predznakom.

Nepoznate varijable (od njih r) koje ostaju na lijevoj strani jednadžbe se pozivaju main.

Nepoznate varijable (ima n - r komada) koje se nalaze na desnoj strani se pozivaju besplatno.

Sada vjerujemo da slobodne nepoznate varijable mogu imati proizvoljne vrijednosti, dok će r glavnih nepoznatih varijabli biti izražene kroz slobodne nepoznate varijable na jedinstven način. Njihov izraz se može naći rješavanjem rezultirajuće SLAE korištenjem Cramerove metode, matrične metode ili Gaussove metode.

Pogledajmo to na primjeru.

Primjer.

Riješiti sistem linearnih algebarskih jednačina .

Rješenje.

Nađimo rang glavne matrice sistema metodom graničenja maloletnika. Uzmimo 1 1 = 1 kao nenulti minor prvog reda. Počnimo tražiti minor koji nije nula drugog reda koji graniči s ovim minorom:


Ovako smo pronašli nenulti minor drugog reda. Počnimo tražiti granični minor koji nije nula trećeg reda:


Dakle, rang glavne matrice je tri. Rang proširene matrice je takođe jednak tri, odnosno sistem je konzistentan.

Za osnovni jedan uzimamo pronađeni minor trećeg reda različit od nule.

Radi jasnoće, prikazujemo elemente koji čine osnovni minor:


Ostavljamo članove uključene u bazni minor na lijevoj strani sistemskih jednačina, a ostatak prenosimo sa suprotnim predznacima na desnu stranu:


Dajmo slobodnim nepoznatim varijablama x 2 i x 5 proizvoljne vrijednosti, odnosno prihvatamo , gdje su proizvoljni brojevi. U ovom slučaju, SLAE će poprimiti oblik


Rešimo rezultirajući elementarni sistem linearnih algebarskih jednadžbi koristeći Cramerovu metodu:


Dakle, .

U svom odgovoru ne zaboravite navesti slobodne nepoznate varijable.

odgovor:

Gdje su proizvoljni brojevi.

Sažmite.

Da bismo riješili sistem općih linearnih algebarskih jednadžbi, prvo utvrđujemo njegovu kompatibilnost koristeći Kronecker–Capelli teorem. Ako rang glavne matrice nije jednak rangu proširene matrice, onda zaključujemo da je sistem nekompatibilan.

Ako je rang glavne matrice jednak rangu proširene matrice, tada biramo bazni minor i odbacujemo jednadžbe sistema koje ne učestvuju u formiranju odabranog baznog minora.

Ako je red baznog minora jednak broju nepoznatih varijabli, tada SLAE ima jedinstveno rješenje, koje se može naći bilo kojom metodom koja nam je poznata.

Ako je red baznog minora manji od broja nepoznatih varijabli, tada na lijevoj strani sistemskih jednačina ostavljamo članove s glavnim nepoznatim varijablama, preostale članove prenosimo na desne strane i dajemo proizvoljne vrijednosti slobodne nepoznate varijable. Iz rezultirajućeg sistema linearnih jednačina nalazimo glavne nepoznate varijable koristeći Cramerovu metodu, matričnu metodu ili Gaussovu metodu.

Gaussova metoda za rješavanje sistema linearnih algebarskih jednačina opšteg oblika.

Gaussova metoda se može koristiti za rješavanje sistema linearnih algebarskih jednačina bilo koje vrste bez prethodnog testiranja njihove konzistentnosti. Proces sekvencijalne eliminacije nepoznatih varijabli omogućava da se izvede zaključak i o kompatibilnosti i o nekompatibilnosti SLAE, a ako rješenje postoji, omogućava ga pronalaženje.

Sa računske tačke gledišta, Gausova metoda je poželjnija.

Detaljan opis i analizirane primjere pogledajte u članku Gausova metoda za rješavanje sistema općih linearnih algebarskih jednačina.

Pisanje opšteg rešenja za homogene i nehomogene linearne algebarske sisteme korišćenjem vektora osnovnog sistema rešenja.

U ovom dijelu ćemo govoriti o istovremenim homogenim i nehomogenim sistemima linearnih algebarskih jednačina koje imaju beskonačan broj rješenja.

Hajde da se prvo pozabavimo homogenim sistemima.

Osnovni sistem rješenja homogeni sistem p linearnih algebarskih jednačina sa n nepoznatih varijabli je skup (n – r) linearno nezavisnih rješenja ovog sistema, gdje je r red baznog minora glavne matrice sistema.

Ako linearno nezavisna rješenja homogene SLAE označimo kao X (1) , X (2) , ..., X (n-r) (X (1) , X (2) , ..., X (n-r) su stupasti matrice dimenzije n sa 1) , onda je opšte rešenje ovog homogenog sistema predstavljeno kao linearna kombinacija vektora osnovnog sistema rešenja sa proizvoljnim konstantnim koeficijentima C 1, C 2, ..., C (n-r), tj. je, .

Šta znači pojam opšte rješenje homogenog sistema linearnih algebarskih jednačina (oroslau)?

Značenje je jednostavno: formula specificira sva moguća rješenja originalnog SLAE, drugim riječima, uzimajući bilo koji skup vrijednosti proizvoljnih konstanti C 1, C 2, ..., C (n-r), koristeći formulu koju ćemo dobiti jedno od rješenja originalne homogene SLAE.

Dakle, ako pronađemo fundamentalni sistem rješenja, onda možemo definirati sva rješenja ove homogene SLAE kao .

Pokažimo proces konstruisanja fundamentalnog sistema rješenja za homogenu SLAE.

Odabiremo bazni minor originalnog sistema linearnih jednadžbi, isključujemo sve ostale jednačine iz sistema i sve članove koji sadrže slobodne nepoznate varijable prenosimo na desnu stranu jednadžbi sistema suprotnih predznaka. Damo slobodnim nepoznatim varijablama vrijednosti 1,0,0,...,0 i izračunajmo glavne nepoznanice rješavanjem rezultirajućeg elementarnog sistema linearnih jednadžbi na bilo koji način, na primjer, korištenjem Cramerove metode. Ovo će rezultirati X (1) - prvim rješenjem fundamentalnog sistema. Ako slobodnim nepoznanicama damo vrijednosti 0,1,0,0,…,0 i izračunamo glavne nepoznanice, dobićemo X (2) . I tako dalje. Ako slobodnim nepoznatim varijablama dodijelimo vrijednosti 0,0,…,0,1 i izračunamo glavne nepoznate, dobićemo X (n-r) . Na taj način će se konstruisati fundamentalni sistem rješenja homogene SLAE i njegovo opšte rješenje može se zapisati u obliku .

Za nehomogene sisteme linearnih algebarskih jednadžbi, opšte rešenje je predstavljeno u obliku , gde je opšte rešenje odgovarajućeg homogenog sistema, a partikularno rešenje originalnog nehomogenog SLAE, koje dobijamo davanjem slobodnim nepoznanicama vrednosti ​​0,0,...,0 i izračunavanje vrijednosti glavnih nepoznanica.

Pogledajmo primjere.

Primjer.

Pronađite osnovni sistem rješenja i opšte rješenje homogenog sistema linearnih algebarskih jednadžbi .

Rješenje.

Rang glavne matrice homogenih sistema linearnih jednačina je uvek jednak rangu proširene matrice. Pronađimo rang glavne matrice metodom graničnih minora. Kao nenulti minor prvog reda, uzimamo element a 1 1 = 9 glavne matrice sistema. Nađimo granični minor koji nije nula drugog reda:

Pronađen je minor drugog reda, različit od nule. Prođimo kroz minore trećeg reda koji se graniče s njim u potrazi za nenultom jedinicom:

Svi granični minori trećeg reda jednaki su nuli, stoga je rang glavne i proširene matrice jednak dva. Hajde da uzmemo. Radi jasnoće, zabilježimo elemente sistema koji ga čine:

Treća jednačina originalne SLAE ne sudjeluje u formiranju baznog minora, stoga se može isključiti:

Ostavljamo članove koji sadrže glavne nepoznanice na desnim stranama jednadžbe, a članove sa slobodnim nepoznanicama prenosimo na desne strane:

Konstruirajmo fundamentalni sistem rješenja originalnog homogenog sistema linearnih jednačina. Osnovni sistem rješenja ove SLAE sastoji se od dva rješenja, pošto originalna SLAE sadrži četiri nepoznate varijable, a red njenog baznog minora je jednak dva. Da bismo pronašli X (1), dajemo slobodnim nepoznatim varijablama vrijednosti x 2 = 1, x 4 = 0, zatim pronađemo glavne nepoznate iz sistema jednačina
.

Očuvanje vaše privatnosti nam je važno. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte našu praksu privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupljati različite informacije, uključujući vaše ime, broj telefona, adresu e-pošte itd.

Kako koristimo vaše lične podatke:

• Lični podaci koje prikupljamo omogućavaju nam da vas kontaktiramo s jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke za slanje važnih obavijesti i komunikacija.
• Lične podatke možemo koristiti i za interne svrhe, kao što su provođenje revizija, analiza podataka i različita istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnoj promociji, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje informacija trećim licima

Podatke koje dobijemo od vas ne otkrivamo trećim licima.

Izuzeci:

• Ako je potrebno - u skladu sa zakonom, sudskim postupkom, u sudskom postupku, i/ili na osnovu javnih zahtjeva ili zahtjeva državnih organa u Ruskoj Federaciji - otkriti vaše lične podatke. Takođe možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnosne, provođenje zakona ili druge svrhe od javnog značaja.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo na odgovarajuću treću stranu.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Poštivanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima prenosimo standarde privatnosti i sigurnosti i striktno provodimo praksu privatnosti.

Većina stvarnih sistema je nelinearna, tj. ponašanje sistema opisano je jednadžbama:

Često se u praksi nelinearni sistemi mogu aproksimirati linearnim sistemima u određenom ograničenom području.

Pretvarajmo se to
jer je jednačina (1) poznata. Zamenimo sistem (1,2) zamenom početnih uslova

Pretpostavljamo da su početna stanja i ulazna varijabla promijenio tako da je novo stanje i ulazna varijabla ima sljedeći oblik.

Izlaz
nalazimo kao rezultat rješavanja poremećenih jednačina.

Proširimo desnu stranu u Taylorov niz.

-termin preostale greške drugog reda malenosti.

Oduzimanjem originalnog rješenja od proširenja dobijamo sljedeće linearizirane jednadžbe:

.

Parcijalne derivate označavamo kao vremenski zavisne koeficijente

Ovi izrazi se mogu prepisati kao

Dobijamo linearizirane jednadžbe u ravnotežnim tačkama
.

. U tački

Rješenje ove jednačine

Hajde da razlikujemo desnu stranu originalne jednadžbe u odnosu na x, dobijamo

.

Hajde da lineariziramo jednačinu za proizvoljnu početnu vrijednost
.

Dobijamo linearizovani sistem u obliku nestacionarne jednačine

Rješenje lineariziranog sistema ima oblik:

.

1.7. Tipične smetnje

Spoljni uznemirujući uticaji mogu biti različite prirode:

trenutno djelovanje u obliku impulsa i konstantno djelovanje.

Ako se razlikuje u vremenu
, To
, stoga (t)-funkcija predstavlja vremenski izvod akcije jednog koraka.

(t) - funkcija kada je integrirana ima sljedeća svojstva filtriranja:

Integrabilni proizvod proizvoljne funkcije
i(t)-funkcije se filtriraju iz svih vrijednosti
samo ono što odgovara trenutku primene trenutnog jediničnog impulsa.

2 U. Sistemi drugog reda

2.1 Svođenje jednačina drugog reda na sisteme jednačina prvog reda

Primjer linearnog stacionarnog sistema.

Drugi opis istog sistema drugog reda dat je parom spregnutih diferencijalnih jednadžbi prvog reda

(2)

pri čemu je odnos između koeficijenata ovih jednačina određen sljedećim relacijama

2.2. Rješavanje jednačina drugog reda

Korištenje diferencijalnog operatora
jednačina se može predstaviti u kompaktnijem obliku

Jednačina (1) se rješava u 3 faze:

1) naći opšte rešenje homogena jednačina;

2) pronaći određeno rješenje ;

3) kompletno rješenje je zbir ova dva rješenja
.

Razmotrimo homogenu jednačinu

tražit ćemo rješenje u formi

(5)

Gdje
stvarna ili kompleksna količina. Zamjenom (5) u (4) dobijamo

(6)

Ovaj izraz je rješenje homogene jednadžbe ako s zadovoljava karakterističnu jednačinu

Za s 1  s 2, rješenje homogene jednačine ima oblik

Zatim tražimo rješenje u formi
i zamjenjujući ga u originalnu jednačinu

Otkud to sledi
.

Ako odaberete

. (8)

Tražimo određeno rješenje izvorne jednadžbe (1) koristeći metodu varijacije
u obliku

Na osnovu (11), (13) dobijamo sistem

Potpuno rješenje jednačine.

Promjenom varijabli dobijamo jednačinu drugog reda:

PHASE PLANE

Dvodimenzionalni prostor stanja ili fazna ravan je ravan u kojoj se razmatraju dvije varijable stanja u pravokutnom koordinatnom sistemu

- ove varijable stanja formiraju vektor
.

G promijeniti raspored
formira putanju kretanja. Potrebno je naznačiti smjer kretanja putanje.

Stanje ravnoteže naziva se takvo stanje , u kojem sistem ostaje pod uslovom da
Stanje ravnoteže može se odrediti (ako postoji) iz relacija

na bilo koji t.

Stanja ravnoteže se ponekad nazivaju kritičnim, fundamentalnim ili nultim tačkama.

Putanja sistema se ne mogu ukrštati u prostoru, što implicira i jedinstvenost rješenja diferencijalne jednačine.

Nijedna putanja ne prolazi kroz stanje ravnoteže, iako se mogu približiti singularnim tačkama proizvoljno bliskim (na
) .

Vrste bodova

1 Regularna tačka je svaka tačka kroz koju trajektorija može proći; ravnotežna tačka nije pravilna.

2. Jedna ravnotežna tačka je izolovana ako njena mala okolina sadrži samo regularne tačke.

Razmotrite sistem

Za određivanje ravnotežnog stanja rješavamo sljedeći sistem jednačina

.

Dobijamo zavisnost između varijabli stanja
.

bilo koja tačka u kojoj je stanje ravnoteže. Ove tačke nisu izolovane.

Imajte na umu da za linearni stacionarni sistem

početno stanje se ispostavlja kao stanje ravnoteže i izolovano ako je determinanta matrice koeficijenata
, Onda
postoji stanje ravnoteže.

Za nelinearni sistem drugog reda, stanje ravnoteže je zove jednostavno, ako odgovarajuća Jakobijanska matrica nije jednaka 0.

Inače država neće biti jednostavna. Ako je ravnotežna tačka jednostavna, onda je izolovana. Obrnuto nije nužno tačno (osim u slučaju linearnih stacionarnih sistema).

Razmotrimo rješenje jednadžbe stanja za linearni sistem drugog reda:
.

Ovaj sistem se može predstaviti sa dve jednačine prvog reda,

označimo
,

Karakteristična jednačina
a rješenje bi bilo:

Rješenje jednačine je zapisano u obliku

Linearne diferencijalne jednadžbe drugog reda

Diferencijalna jednadžba drugog reda ima oblik .

Definicija. Opće rješenje jednačine drugog reda je funkcija koja je, za bilo koju vrijednost, rješenje ove jednačine.

Definicija. Linearna homogena jednačina drugog reda naziva se jednačina. Ako su koeficijenti konstantni, tj. ne zavise od , onda se ova jednadžba naziva jednadžba s konstantnim koeficijentima i piše se na sljedeći način: .

Jednačinu ćemo nazvati linearnom nehomogenom jednačinom.

Definicija. Jednadžba koja se dobije iz linearne homogene jednadžbe zamjenom funkcije jedinicom i odgovarajućim potencijama naziva se karakteristična jednačina.

Poznato je da kvadratna jednadžba ima rješenje u zavisnosti od diskriminanta: , tj. ako , tada su korijeni i različiti realni brojevi. Ako onda. Ako, tj. , tada će biti imaginarni broj, a korijeni i bit će kompleksni brojevi. U ovom slučaju, slažemo se da označimo .

Primjer 4. Riješite jednačinu.

Rješenje. Diskriminanta ove kvadratne jednadžbe je dakle .

Pokazat ćemo kako pronaći opšte rješenje homogene linearne jednadžbe drugog reda koristeći formu korijena karakteristične jednadžbe.

Ako su pravi korijeni karakteristične jednadžbe, onda .

Ako su korijeni karakteristične jednadžbe isti, tj. , onda se opće rješenje diferencijalne jednadžbe traži pomoću formule ili .

Ako karakteristična jednadžba ima kompleksne korijene, onda.

Primjer 5. Naći opće rješenje jednačine.

Rješenje. Napravimo karakterističnu jednačinu za ovu diferencijalnu jednačinu: . Njegovi korijeni su valjani i različiti. Stoga je generalno rješenje .

Osnovni sistem rješenja linearne homogene diferencijalne jednadžbe. Teorema o strukturi općeg rješenja rješenja linearne homogene diferencijalne jednadžbe. U ovom dijelu ćemo dokazati da osnova linearnog prostora parcijalnih rješenja homogene jednadžbe može biti bilo koji skup n njena linearno nezavisna rješenja.
Def. 14.5.5.1. fundamentalni sistem rješenja. Osnovni sistem rješenja linearna homogena diferencijalna jednadžba n -ti red je bilo koji linearno nezavisan sistem y 1 (x ), y 2 (x ), …, y n (x ) njegov n privatna rješenja.
Teorema 14.5.5.1.1 o strukturi opšteg rješenja linearne homogene diferencijalne jednadžbe. Zajednička odluka y (x ) linearne homogene diferencijalne jednadžbe je linearna kombinacija funkcija iz osnovnog sistema rješenja ove jednadžbe:
y (x ) = C 1 y 1 (x ) + C 2 y 2 (x ) + …+ C n y n (x ).
Dokument. Neka y 1 (x ), y 2 (x ), …, y n (x ) je osnovni sistem rješenja linearne homogene diferencijalne jednačine. Potrebno je dokazati da bilo koje posebno rješenje y šta ( x ) ove jednačine sadržana je u formuli y (x ) = C 1 y 1 (x ) + C 2 y 2 (x ) + …+ C n y n (x ) za određeni skup konstanti C 1 , C 2 , …, Cn . Uzmimo bilo koju tačku, izračunajmo brojeve u ovoj tački i pronađemo konstante C 1 , C 2 , …, Cn kao rješenje linearnog nehomogenog sistema algebarskih jednačina
Takvo rješenje postoji i jedinstveno je, jer je determinanta ovog sistema jednaka . Razmotrite linearnu kombinaciju y (x ) = C 1 y 1 (x ) + C 2 y 2 (x ) + …+ C n y n (x ) funkcije iz osnovnog sistema rješenja sa ovim vrijednostima konstanti C 1 , C 2 , …, Cn i uporedi ga sa funkcijom y šta ( x ). Funkcije y (x ) I y šta ( x ) zadovoljavaju istu jednačinu i iste početne uslove u tački x 0, dakle, zbog jedinstvenosti rješenja Cauchyjevog problema, poklapaju se: y šta ( x ) = C 1 y 1 (x ) + C 2 y 2 (x ) + … + C n y n (x ). Teorema je dokazana.
Iz ove teoreme slijedi da dimenzija linearnog prostora parcijalnih rješenja homogene jednadžbe sa kontinuiranim koeficijentima ne prelazi n . Ostaje dokazati da ova dimenzija nije manja od n .
Teorema 14.5.5.1.2 o postojanju fundamentalnog sistema rješenja linearne homogene diferencijalne jednačine. Bilo koja linearna homogena diferencijalna jednadžba n reda sa kontinuiranim koeficijentima ima fundamentalni sistem rješenja, tj. sistem od n linearno nezavisna rješenja.
Dokument. Uzmimo bilo koju numeričku odrednicu n -ti red, nije jednak nuli