Табличні значення синусів та косінусів. Тригонометричні функції
Поняття синуса (), косинуса (), тангенса (), котангенса () нерозривно пов'язані з поняттям кута. Щоб добре розібратися в цих, на перший погляд, складних поняттях (які викликають у багатьох школярів стан жаху), і переконатися, що «не такий страшний чорт, як його малюють», почнемо від початку і розберемося в понятті кута.
Поняття кута: радіан, градус
Давай подивимося малюнку. Вектор "повернувся" щодо точки на певну величину. Так ось мірою цього повороту щодо початкового положення і виступатиме кут.
Що ще необхідно знати про поняття кута? Ну, звичайно ж, одиниці виміру кута!
Кут, як і геометрії, і у тригонометрії, може вимірюватися у градусах і радіанах.
Кутом (один градус) називають центральний кут в колі, що спирається на кругову дугу, рівну частині кола. Таким чином, все коло складається з «шматочків» кругових дуг, або кут, що описується колом, дорівнює.

Тобто малюнку вище зображений кут, рівний, тобто цей кут спирається на кругову дугу розміром довжини кола.
Кутом у радіан називають центральний кут в колі, що спирається на кругову дугу, довжина якої дорівнює радіусу кола. Ну що, розібрався? Якщо ні, то давай розумітися на малюнку.

Отже, малюнку зображений кут, рівний радіану, тобто цей кут спирається на кругову дугу, довжина якої дорівнює радіусу кола (довжина дорівнює довжині або радіус дорівнює довжині дуги). Таким чином, довжина дуги обчислюється за такою формулою:
Де – центральний кут у радіанах.
Ну що, можеш, знаючи це, відповісти, скільки радіан містить кут, який описує коло? Так, для цього треба згадати формулу довжини кола. Ось вона:
Ну ось, тепер співвіднесемо ці дві формули і отримаємо, що кут, що описується коло дорівнює. Тобто, співвіднісши величину у градусах та радіанах, отримуємо, що. Відповідно, . Як можна побачити, на відміну «градусів», слово «радіан» опускається, оскільки одиниця виміру зазвичай зрозуміла з контексту.
А скільки радіан складають? Все правильно!
Вловив? Тоді вперед закріплювати:
Виникли проблеми? Тоді дивись відповіді:
Прямокутний трикутник: синус, косинус, тангенс, котангенс кута
Отже, з поняттям кута розібралися. А що ж таке синус, косинус, тангенс, котангенс кута? Давай розбиратись. Для цього нам допоможе прямокутний трикутник.

Як називаються сторони прямокутного трикутника? Все вірно, гіпотенуза і катети: гіпотенуза - це сторона, що лежить навпроти прямого кута (у прикладі це сторона); катети - це дві сторони, що залишилися і (ті, що прилягають до прямого кута), причому, якщо розглядати катети щодо кута, то катет - це прилеглий катет, а катет - протилежний. Отже, тепер дамо відповідь на запитання: що таке синус, косинус, тангенс і котангенс кута?
Синус кута- Це ставлення протилежного (далекого) катета до гіпотенузи.
У нашому трикутнику.
Косинус кута- Це ставлення прилеглого (близького) катета до гіпотенузи.
У нашому трикутнику.
Тангенс кута- Це ставлення протилежного (далекого) катета до прилеглого (близького).
У нашому трикутнику.
Котангенс кута- Це ставлення прилеглого (близького) катета до протилежного (дальнього).
У нашому трикутнику.
Ці визначення необхідні запам'ятати! Щоб було простіше запам'ятати який катет на що ділити, необхідно чітко усвідомити, що в тангенсеі котангенсісидять тільки катети, а гіпотенуза з'являється тільки в синусіі косинус. А далі можна придумати ланцюжок асоціацій. Наприклад, ось таку:
Косинус→торкатися→доторкнутися→прилежний;
Котангенс→торкатися→доторкнутися→прилежний.
Насамперед, необхідно запам'ятати, що синус, косинус, тангенс і котангенс як відносини сторін трикутника не залежить від довжин цих сторін (при одному вугіллі). Чи не віриш? Тоді переконайся, подивившись на малюнок:

Розглянемо, наприклад, косинус кута. За визначенням, з трикутника: , але ми можемо обчислити косинус кута і з трикутника: . Бачиш, довжини у сторін різні, а значення косинуса одного кута одне й те саме. Таким чином, значення синуса, косинуса, тангенсу та котангенсу залежать виключно від величини кута.
Якщо розібрався у визначеннях, то вперед закріплюйте їх!
Для трикутника, зображеного нижче малюнку, знайдемо.

Ну що, вловив? Тоді пробуй сам: порахуй те саме для кута.
Одиничне (тригонометричне) коло
Розбираючись у поняттях градуса і радіана, ми розглядали коло з рівним радіусом. Таке коло називається одиничною. Вона дуже знадобиться щодо тригонометрії. Тому зупинимося на ній трохи докладніше.

Як можна помітити, це коло побудовано в декартовій системі координат. Радіус кола дорівнює одиниці, при цьому центр кола лежить на початку координат, початкове положення радіус-вектора зафіксовано вздовж позитивного напрямку осі (у нашому прикладі, це радіус).
Кожній точці кола відповідають два числа: координата по осі та координата по осі. А що це за числа-координати? І взагалі, яке відношення вони мають до цієї теми? Для цього треба згадати розглянутий прямокутний трикутник. На малюнку, наведеному вище, можна помітити цілих два прямокутні трикутники. Розглянемо трикутник. Він прямокутний, оскільки є перпендикуляром до осі.
Чому дорівнює трикутнику? Все правильно. Крім того, нам відомо, що - це радіус одиничного кола, а значить, . Підставимо це значення на нашу формулу для косинуса. Ось що виходить:
А чому дорівнює трикутнику? Ну звичайно,! Підставимо значення радіуса в цю формулу та отримаємо:
Так, а можеш сказати, які координати має точка, що належить колу? Ну що, аж ніяк? А якщо збагнути, що й – це просто числа? Який координаті відповідає? Ну, звісно, координати! А якій координаті відповідає? Все правильно, координаті! Таким чином, точка.

А чому тоді рівні? Все вірно, скористаємося відповідними визначеннями тангенсу та котангенсу і отримаємо, що, а.
А що, якщо кут буде більшим? Ось, наприклад, як у цьому рисунку:

Що ж змінилося у цьому прикладі? Давай розбиратись. Для цього знову звернемося до прямокутного трикутника. Розглянемо прямокутний трикутник: кут (як прилеглий до кута). Чому дорівнює значення синуса, косинуса, тангенсу та котангенсу для кута? Все вірно, дотримуємося відповідних визначень тригонометричних функцій:
Ну от, як бачиш, значення синуса кута так само відповідає координаті; значення косинуса кута – координаті; а значення тангенсу та котангенсу відповідним співвідношенням. Таким чином, ці співвідношення можна застосовувати до будь-яких поворотів радіус-вектора.
Вже згадувалося, що початкове становище радіус-вектора - вздовж позитивного спрямування осі. Досі ми обертали цей вектор проти годинникової стрілки, а що буде, якщо повернути його за годинниковою стрілкою? Нічого екстраординарного, вийде так само кут певної величини, але він буде негативним. Таким чином, при обертанні радіус-вектора проти годинникової стрілки виходять позитивні кути, а при обертанні за годинниковою стрілкою - негативні.
Отже, ми знаємо, що цілий оберт радіус-вектора по колу становить або. А чи можна повернути радіус-вектор на чи на? Ну звісно, можна! У першому випадку, таким чином, радіус-вектор зробить один повний оборот і зупиниться в положенні.
У другому випадку, тобто радіус-вектор зробить три повні обороти і зупиниться в положенні або.
Таким чином, з наведених прикладів можемо зробити висновок, що кути, що відрізняються на або (де - будь-яке ціле число), відповідають одному положенню радіус-вектора.
Нижче на малюнку зображено кут. Це зображення відповідає куту тощо. Цей список можна продовжити до безкінечності. Всі ці кути можна записати загальною формулою або (де – будь-яке ціле число)

Тепер, знаючи визначення основних тригонометричних функцій та використовуючи одиничне коло, спробуй відповісти, чому рівні значення:
Ось тобі на допомогу одиничне коло:

Виникли проблеми? Тоді давай розбиратись. Отже, ми знаємо, що:
Звідси ми визначаємо координати точок, що відповідають певним заходам кута. Ну що ж, почнемо по порядку: кутку відповідає точка з координатами, отже:
Немає;
Далі, дотримуючись тієї ж логіки, з'ясовуємо, що кутам відповідають точки з координатами, відповідно. Знаючи це, легко визначити значення тригонометричних функцій у відповідних точках. Спочатку спробуй сам, а потім звіряйся з відповідями.
Відповіді:
Не існує
Не існує
Не існує
Не існує
Таким чином, ми можемо скласти таку табличку:

Немає потреби пам'ятати всі ці значення. Достатньо пам'ятати відповідність координат точок на одиничному колі та значень тригонометричних функцій:
А ось значення тригонометричних функцій кутів і, наведених нижче в таблиці, необхідно запам'ятати:

Не треба лякатися, зараз покажемо один із прикладів досить простого запам'ятовування відповідних значень:
Для користування цим методом життєво необхідно запам'ятати значення синуса для всіх трьох заходів кута (), а також значення тангенсу кута. Знаючи ці значення, досить просто відновити всю таблицю цілком - значення косинуса переносяться відповідно до стрілочок, тобто:
Знаючи це можна відновити значення. Чисельник « » буде відповідати, а знаменник « » відповідає. Значення котангенсу переносяться відповідно до стрілок, вказаних на малюнку. Якщо це усвідомити і запам'ятати схему зі стрілочками, достатньо пам'ятати всього значення з таблиці.
Координати точки на колі
А чи можна знайти точку (її координати) на колі, знаючи координати центру кола, його радіус та кут повороту?
Ну, звісно, можна! Давай виведемо загальну формулу для знаходження координат точки.
Ось, наприклад, перед нами таке коло:

Нам дано, що точка – центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, одержаної поворотом точки на градусів.
Як очевидно з малюнка, координаті точки відповідає довжина відрізка. Довжина відрізка відповідає координаті центру кола, тобто дорівнює. Довжину відрізка можна виразити, використовуючи визначення косинуса:
Тоді маємо, що для точки координат.
За тією ж логікою знаходимо значення координати для точки. Таким чином,
Отже, у загальному вигляді координати точок визначаються за формулами:
Координати центру кола,
Радіус кола,
Кут повороту вектор радіуса.
Як можна помітити, для одиничного кола, що розглядається нами, ці формули значно скорочуються, так як координати центру дорівнюють нулю, а радіус дорівнює одиниці:
Ну що, спробуємо ці формули на смак, повправляючись у знаходженні крапок на колі?
1. Знайти координати точки на одиничному колі, отриманому поворотом точки на.
2. Знайти координати точки на одиничному колі, отриманому поворотом точки на.
3. Знайти координати точки на одиничному колі, отриманому поворотом точки на.
4. Крапка - центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, отриманої поворотом початкового радіус-вектора.
5. Крапка - центр кола. Радіус кола дорівнює. Необхідно знайти координати точки, отриманої поворотом початкового радіус-вектора.
Виникли проблеми у знаходженні координот точки на колі?
Розв'яжи ці п'ять прикладів (або добре розберись у рішенні) і ти навчишся їх знаходити!
1.
Можна зауважити, що. Адже ми знаємо, що відповідає повному обороту початкової точки. Таким чином, точка, що шукається, буде знаходитися в тому ж положенні, що і при повороті на. Знаючи це, знайдемо шукані координати точки:
2. Окружність одинична з центром у точці, отже, ми можемо скористатися спрощеними формулами:
Можна зауважити, що. Ми знаємо, що відповідає двом повним оборотам початкової точки. Таким чином, точка, що шукається, буде знаходитися в тому ж положенні, що і при повороті на. Знаючи це, знайдемо шукані координати точки:
Синус та косинус – це табличні значення. Згадуємо їх значення та отримуємо:
Таким чином, потрібна точка має координати.
3. Окружність одинична з центром у точці, отже, ми можемо скористатися спрощеними формулами:
Можна зауважити, що. Зобразимо приклад на малюнку:

Радіус утворює з віссю кути, рівні та. Знаючи, що табличні значення косинуса та синуса рівні, і визначивши, що косинус тут набуває негативного значення, а синус позитивне, маємо:
Докладніше такі приклади розбираються щодо формул приведення тригонометричних функцій у темі .
Таким чином, потрібна точка має координати.
4.
Кут повороту радіуса вектора (за умовою)
Для визначення відповідних знаків синуса та косинуса побудуємо одиничне коло та кут:

Як можна побачити, значення, тобто позитивно, а значення, тобто – негативно. Знаючи табличні значення відповідних тригонометричних функцій, отримуємо, що:
Підставимо отримані значення в нашу формулу і знайдемо координати:
Таким чином, потрібна точка має координати.
5. Для вирішення цього завдання скористаємося формулами у загальному вигляді, де
Координати центру кола (у нашому прикладі,
Радіус кола (за умовою,)
Кут повороту векторного радіуса (за умовою,).
Підставимо всі значення у формулу та отримаємо:
та - табличні значення. Згадуємо та підставляємо їх у формулу:
Таким чином, потрібна точка має координати.
КОРОТКИЙ ВИКЛАД І ОСНОВНІ ФОРМУЛИ
Синус кута - це відношення протилежного (далекого) катета до гіпотенузи.
Косинус кута – це відношення прилеглого (близького) катета до гіпотенузи.
Тангенс кута - це відношення протилежного (далекого) катета до прилеглого (близького).
Котангенс кута - це відношення прилеглого (близького) катета до протилежного (далекого).
Увага!
До цієї теми є додаткові
матеріали у розділі 555.
Для тих, хто сильно "не дуже..."
І для тих, хто "дуже навіть...")
Насамперед нагадаю простий, але дуже корисний висновок з уроку "Що таке синус та косинус? Що таке тангенс та котангенс?"
Ось цей висновок:
Синус, косинус, тангенс та котангенс міцно пов'язані зі своїми кутами. Знаємо одне – значить, знаємо й інше.
Іншими словами, кожен кут має свій незмінний синус і косинус. І майже у кожного – свій тангенс та котангенс. Чому майже?Про це нижче.
Це знання чудово допомагає в навчанні! Існує маса завдань, де потрібно перейти від синусів до кутів і навпаки. Для цього існує таблиці синусів.Аналогічно, для завдань із косинусом - таблиці косінусів.І, як ви вже здогадалися, існує таблиця тангенсіві таблиця котангенсів.)
Таблиці бувають різні. Довгі, де можна подивитися, до чого дорівнює, скажімо, sin37°6'. Розкриваємо таблиці Брадіса, шукаємо кут тридцять сім градусів шість хвилин і бачимо значення 0,6032. Зрозуміло, запам'ятовувати це число (і тисячі інших табличних значень) не потрібно.
По суті, в наш час довгі таблиці косінусів синусів тангенсів котангенсів не надто й потрібні. Один гарний калькулятор замінює їх повністю. Але знати існування таких таблиць не заважає. Для загальної ерудиції.)
І навіщо тоді цей урок? - Запитайте ви.
А ось навіщо. Серед нескінченної кількості кутів є особливі,про які ви повинні знати все. На цих кутах побудовано всю шкільну геометрію і тригонометрію. Це, свого роду, "таблиця множення" тригонометрії. Якщо ви не знаєте, чому дорівнює, наприклад sin50°, ніхто вас не засудить.) Але якщо ви не знаєте, чому дорівнює sin30°, будьте готові отримати заслужену двійку...
Таких особливихкутів теж пристойно набирається. Шкільні підручники зазвичай люб'язно пропонують до запам'ятовування таблицю синусів та таблицю косинусівдля сімнадцяти кутів. Ну і, зрозуміло, таблицю тангенсів та таблицю котангенсівдля тих самих сімнадцяти кутів... Тобто. пропонується запам'ятати 68 значень. Які, між іншим, дуже схожі між собою, раз у раз повторюються і змінюють знаки. Для людини без ідеальної зорової пам'яті - та ще завдання ...)
Ми підемо іншим шляхом. Замінимо механічне запам'ятовування на логіку та кмітливість. Тоді нам доведеться зазубрити 3 (три!) значення для таблиці синусів та таблиці косінусів. І 3 (три!) Значення для таблиці тангенсів та таблиці котангенсів. І все. Шість значень запам'ятати легше, ніж 68, мені здається...)
Всі інші необхідні значення ми отримуватимемо з цих шести за допомогою потужної законної шпаргалки - Тригонометричного кола. Якщо ви не вивчали цю тему, сходіть за посиланням, не лінуйтеся. Це коло не тільки для цього уроку потрібне. Він незамінний для всієї тригонометрії відразу. Чи не користуватися таким інструментом просто гріх! Чи не хочете? Справа ваша. Завчайте таблиці синусів. Таблицю косінусів. Таблиця тангенсів. Таблиця котангенсів.Усі 68 значень для різноманітних кутів.)
Отже, почнемо. Для початку розіб'ємо всі ці спеціальні кути на три групи.
Перша група кутів.
Розглянемо першу групу кутів із сімнадцяти особливих. Це 5 кутів: 0 °, 90 °, 180 °, 270 °, 360 °.
Ось так виглядає таблиця синусів косинусів тангенсів котангенсів для цих кутів:
Кут х
|
0 |
90 |
180 |
270 |
360 |
Кут х
|
0 |
||||
sin x |
0 |
1 |
0 |
-1 |
0 |
cos x |
1 |
0 |
-1 |
0 |
1 |
tg x |
0 |
не сущ. |
0 |
не сущ. |
0 |
ctg x |
не сущ. |
0 |
не сущ. |
0 |
не сущ. |
Охочі запам'ятати - запам'ятовуйте. Але одразу скажу, що всі ці одиниці та нулики дуже плутаються в голові. Набагато сильніше, ніж хочеться.) Тому включаємо логіку та тригонометричне коло.
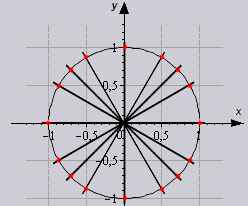
Малюємо коло і відзначаємо на ньому ці самі кути: 0 °, 90 °, 180 °, 270 °, 360 °. Я ці кути відзначив червоними крапками:

Відразу видно, у чому особливість цих кутів. Так! Це кути, які потрапляють точно на осі координат!Власне, тому і плутається народ... Але ми плутатися не будемо. Розберемося, як шукати тригонометричні функції цих кутів без особливого запам'ятовування.
До речі, положення кута 0 градусів повністю збігаєтьсяз положенням кута 360 градусів. Це означає, що синуси, косинуси, тангенси цих кутів абсолютно однакові. Кут 360 градусів я відзначив, щоб замкнути коло.
Припустимо, у складній стресовій обстановці ЄДІ ви якось засумнівалися... Чому дорівнює синус 0 градусів? Наче нуль... А раптом одиниця?! Механічне запам'ятовування така штука. У суворих умовах сумніви є починають...)
Спокій, тільки спокій!) Я підкажу вам практичний прийом, який видасть стовідсотково правильну відповідь і повністю прибере всі сумніви.
Як приклад розберемося, як чітко та надійно визначити, скажімо, синус 0 градусів. А заразом, і косинус 0. Саме в цих значеннях, як не дивно, часто люди плутаються.
Для цього на колі намалюємо довільнийкут х. У першій чверті щоб недалеко від 0 градусів було. Відзначимо на осях синус та косинус цього кута х,все чин-чинарем. Ось так:
А тепер – увага! Зменшимо кут х, наближемо рухливий бік до осі ОХ. Наведіть курсор на зображення (або торкніться зображення на планшеті) і все побачите.
Тепер включаємо елементарну логіку!Дивимося та розмірковуємо: як поводиться sinx при зменшенні кута х? При наближенні кута до нуля?Він зменшується! А cosx – збільшується!Залишається збагнути, що станеться з синусом, коли кут зникне зовсім? Коли рухома сторона кута (точка А) уляжеться на вісь ОХ і кут стане рівним нулю? Очевидно, і синус кута піде в нуль. А косинус збільшиться до... до... Чому дорівнює довжина рухомого боку кута (радіус тригонометричного кола)? Одиниці!
Ось і відповідь. Синус 0 градусів дорівнює 0. Косинус 0 градусів дорівнює 1. Цілком залізно і без жодних сумнівів!) Просто тому, що інакше бути не може.
Абсолютно аналогічно можна дізнатися (або уточнити) синус 270 градусів, наприклад. Або косинус 180. Намалювати коло, довільнийкут в чверті поряд з віссю координат, що цікавить нас, подумки спонукати бік кута і вловити, чим стане синус і косинус, коли сторона кута вляжеться на вісь. Ось і все.
Як бачите, для цієї групи кутів нічого заучувати не треба. Не потрібна тут таблиця синусів...Та й таблиця косінусів- теж.) До речі, після кількох застосувань тригонометричного кола всі ці значення запам'ятаються самі собою. А якщо забудуться – намалював за 5 секунд коло та уточнив. Куди простіше, ніж дзвонити другові з туалету з ризиком для атестату, правда?)
Що стосується тангенсу і котангенсу - все те саме. Малюємо на колі лінію тангенсу (котангенсу) – і все відразу видно. Де вони дорівнюють нулю, а де - не існують. Що, не знаєте про лінії тангенсу та котангенсу? Це сумно, але можна виправити.) Відвідали Розділ 555 Тангенс і котангенс на тригонометричному колі - і немає проблем!
Якщо ви зрозуміли, як чітко визначити синус, косинус, тангенс та котангенс для цих п'яти кутів – я вас вітаю! Про всяк випадок повідомляю, що ви тепер можете визначати функції будь-яких кутів, що потрапляють на осі.А це і 450 °, і 540 °, і 1800 °, і ще нескінченна кількість ...) Відрахував (правильно!) Кут на колі - і немає проблем з функціями.
Але саме з відрахуванням кутів і трапляються проблеми та помилки... Як їх уникнути, написано в уроці: Як намалювати (відрахувати) будь-який кут на тригонометричному колі в градусах. Елементарно, але дуже допомагає у боротьбі з помилками.)
А ось урок: Як намалювати (відрахувати) будь-який кут на тригонометричному колі в радіанах – крутіше буде. У сенсі можливостей. Скажімо, визначити, на яку з чотирьох півосей потрапляє кут
ви зможете за кілька секунд. Я не жартую! Саме за кілька секунд. Ну, звичайно, не тільки 345 "пі"...) І 121, і 16, і -1345. Будь-який цілий коефіцієнт підходить для миттєвої відповіді.
А якщо кут
Подумаєш! Вірна відповідь виходить секунд за 10. Для будь-якого дробового значення радіанів із двійкою у знаменнику.
Власне, цим і добре тригонометричне коло. Тим, що вміння працювати з деякимикутами він автоматично розширює на безлічкутів.
Отже, з п'ятьма кутами із сімнадцяти – розібралися.
Друга група кутів.
Наступна група кутів - це кути 30 °, 45 ° і 60 °. Чому саме ці, а не, наприклад, 20, 50 та 80? Так якось склалося так... Історично.) Далі буде видно, чим гарні ці кути.
Таблиця синусів косинусів тангенсів котангенсів для цих кутів виглядає так:
Кут х
|
0 |
30 |
45 |
60 |
90 |
Кут х
|
0 |
||||
sin x |
0 |
1 |
|||
cos x |
1 |
0 |
|||
tg x |
0 |
1 |
не сущ. |
||
ctg x |
не сущ. |
1 |
0 |
Я залишив значення для 0° та 90° з попередньої таблиці для завершеності картини.) Щоб було видно, що ці кути лежать у першій чверті та зростають. Від 0 до 90. Це стане нам у нагоді далі.
Значення таблиці для кутів 30°, 45° та 60° слід запам'ятати. Зазубрити, якщо хочете. Але і тут є можливість полегшити собі життя. Зверніть увагу на значення таблиці синусівцих кутів. І порівняйте зі значеннями таблиці косінусів...
Так! Вони одні й ті самі!Тільки розташовані у зворотному порядку. Кути зростають (0, 30, 45, 60, 90) - та значення синуса зростаютьвід 0 до 1. Ви можете переконатися з калькулятором. А значення косинуса - спадаютьвід 1 до нуля. Причому самі значення одні й самі.Для кутів 20, 50, 80 так би не вийшло...
Звідси корисний висновок. Достатньо вивчити тризначення для кутів 30, 45, 60 градусів. І пам'ятати, що у синуса вони зростають, а у косинуса – зменшуються. Назустріч синусу.) На половині шляху (45 °) вони зустрічаються, тобто синус 45 градусів дорівнює косінус 45 градусів. А далі знову розходяться... Три значення можна вивчити, правда?
З тангенсами - котангенсами картина виключно та сама. Один на один. Лише значення інші. Ці значення (ще три!) теж треба вивчити.
Ну ось, практично все запам'ятовування закінчилося. Ви зрозуміли (сподіваюся), як визначати значення для п'яти кутів на осі і вивчили значення для кутів 30, 45, 60 градусів. Усього 8.
Залишилося розібратися з останньою групою із 9 кутів.
Ось ці кути:
120 °; 135 °; 150 °; 210 °; 225 °; 240 °; 300 °; 315 °; 330 °. Для цих кутів треба залізно знати таблицю синусів, таблицю косінусів тощо.
Кошмар, правда?)
А якщо додати сюди кути, типу: 405 °, 600 °, або 3000 ° і багато-багато такого ж красивого?)
Чи кути у радіанах? Наприклад, про кути:

і багато інших, ви повинні знати все.
Найцікавіше, що знати це все - неможливо у принципі.Якщо використати механічну пам'ять.
І дуже легко, фактично елементарно – якщо використовувати тригонометричне коло. Якщо ви освоїте практичну роботу з тригонометричним колом, всі ці жахливі кути в градусах будуть легко і елегантно зводитися до старих добрих:
До речі, у мене є ще кілька цікавих сайтів для Вас.)
Можна потренуватися у вирішенні прикладів та дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося – з інтересом!)
можна познайомитися з функціями та похідними.
Довідкові дані щодо тангенсу (tg x) та котангенсу (ctg x). Геометричне визначення, характеристики, графіки, формули. Таблиця тангенсів та котангенсів, похідні, інтеграли, розкладання до лав. Вирази через комплексні змінні. Зв'язок із гіперболічними функціями.
Геометричне визначення

|BD| - Довжина дуги кола з центром у точці A .
α - кут, виражений у радіанах.
Тангенс ( tg α) - це тригонометрична функція, яка залежить від кута між гіпотенузою і катетом прямокутного трикутника, що дорівнює відношенню довжини протилежного катета |BC| до довжини прилеглого катета | AB | .
Котангенс ( ctg α) - це тригонометрична функція, яка залежить від кута між гіпотенузою і катетом прямокутного трикутника, що дорівнює відношенню довжини прилеглого катета |AB| до довжини протилежного катета | BC | .
Тангенс
Де n- ціле.
У західній літературі тангенс позначається так:
.
;
;
.
Графік функції тангенсу, y = tg x

Котангенс
Де n- ціле.
У західній літературі котангенс позначається так:
.
Також прийнято такі позначення:
;
;
.
Графік функції котангенсу, y = ctg x

Властивості тангенсу та котангенсу
Періодичність
Функції y = tg xта y = ctg xперіодичні з періодом π.
Парність
Функції тангенс та котангенс - непарні.
Області визначення та значень, зростання, спадання
Функції тангенс і котангенс безперервні у своїй області визначення (див. доказ безперервності). Основні властивості тангенсу та котангенсу представлені в таблиці ( n- ціле).
| y = tg x | y = ctg x | |
| Область визначення та безперервність | ||
| Область значень | -∞ < y < +∞ | -∞ < y < +∞ |
| Зростання | - | |
| Зменшення | - | |
| Екстремуми | - | - |
| Нулі, y = 0 | ||
| Точки перетину з віссю ординат, x = 0 | y = 0 | - |
Формули
Вирази через синус та косинус
;
;
;
;
;
Формули тангенсу та котангенс від суми та різниці
Інші формули легко отримати, наприклад
Твір тангенсів
Формула суми та різниці тангенсів
У цій таблиці представлені значення тангенсів та котангенсів при деяких значеннях аргументу. 
Вирази через комплексні числа
Вирази через гіперболічні функції
;
;
Похідні
; .
.
Похідна n-го порядку змінної x від функції :
.
Виведення формул для тангенсу >>>; для котангенсу > > >
Інтеграли
Розкладання до лав
Щоб отримати розкладання тангенса за ступенями x, потрібно взяти кілька членів розкладання в степеневий ряд для функцій sin xі cos xі розділити ці багаточлени один на одного, . При цьому виходять такі формули.
При .
при .
де B n- Числа Бернуллі. Вони визначаються або з рекурентного співвідношення:
;
;
де.
Або за формулою Лапласа: 
Зворотні функції
Зворотними функціями до тангенсу та котангенсу є арктангенс та арккотангенс відповідно.
Арктангенс, arctg
, де n- ціле.
Арккотангенс, arcctg
, де n- ціле.
Використана література:
І.М. Бронштейн, К.А. Семендяєв, Довідник з математики для інженерів та учнів втузів, «Лань», 2009.
Г. Корн, Довідник з математики для науковців та інженерів, 2012.
У статті ми повністю розберемося, як виглядає таблиця тригонометричних значень, синуса, косинуса, тангенсу та котангенсу. Розглянемо основне значення тригонометричних функцій, від кута 0,30,45,60,90,...,360 градусів. І подивимося як користуватись даними таблицями у обчисленні значення тригонометричних функцій.
Першою розглянемо таблицю косинуса, синуса, тангенсу та котангенсувід кута в 0, 30, 45, 60, 90, .. градусів. Визначення даних величин дають визначити значення функцій кутів 0 і 90 градусів:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, котангенс від 00 буде невизначеним
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс від 90 0 буде невизначеним
Якщо взяти прямокутні трикутники кути яких від 30 до 90 градусів. Отримаємо:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Зобразимо всі отримані значення як тригонометричної таблиці:
Таблиця синусів, косінусів, тангенсів та котангенсів!
Якщо використовувати формулу приведення, то наша таблиця збільшиться, додадуться значення для кутів до 360 градусів. Виглядатиме вона як:

Також виходячи з властивостей періодичності таблицю можна збільшити, якщо замінимо кути на 0 0 +360 0 *z .... 330 0 +360 0 *z, в якому z є цілим числом. У цій таблиці можна визначити значення всіх кутів, відповідними точками в єдиному колі.
Розберемо наочно використовувати таблицю у рішенні.
Все дуже просто. Оскільки необхідне значення лежить у точці перетину необхідних нам осередків. Наприклад візьмемо cos кута 60 градусів, у таблиці це буде виглядати як:

У підсумковій таблиці основних значень тригонометричних функцій діємо так само. Але в цій таблиці можна дізнатися скільки складе тангенс від кута в 1020 градусів, він = -√3 Перевіримо 1020 0 = 300 0 +360 0 *2. Знайдемо за таблицею.

Таблиця Брадіса. Для синуса, косинуса, тангенсу та котангенсу.
Таблиці Брадіса поділені на кілька частин, складаються з таблиць косинуса та синуса, тангенсу та котангенсу - яка поділена на дві частини (tg кута до 90 градусів і ctg малих кутів).
Синус та косинус


tg кута з 00 закінчуючи 760, ctg кута з 140 закінчуючи 900.


tg до 900 та ctg малих кутів.
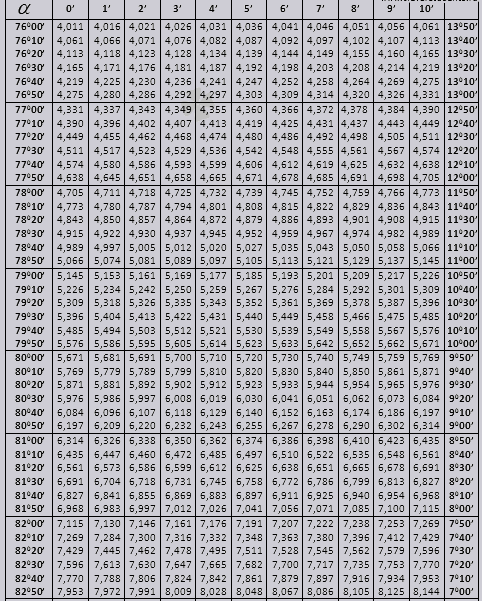

Розберемося як користуватися таблицями Брадіса у вирішенні завдань.
Знайдемо позначення sin (позначення в стовпці з лівого краю) 42 хвилини (позначення знаходиться на верхньому рядку). Шляхом перетину шукаємо позначення, воно = 0,3040.
Величини хвилин вказані з проміжком у шість хвилин, як бути, якщо потрібне нам значення потрапить саме в цей проміжок. Візьмемо 44 хвилини, а в таблиці є тільки 42. Беремо за основу 42 і скористаємося додатковими стовпцями в правій стороні, беремо 2 поправку і додаємо до 0,3040 + 0,0006, отримуємо 0,3046.
При sin 47 хв беремо за основу 48 хв і віднімаємо від неї 1 поправку, тобто 0,3057 - 0,0003 = 0,3054
При обчисленні cos працюємо аналогічно sin тільки за основу беремо нижній рядок таблиці. Наприклад cos 20 0 = 0.9397
Значення tg кута до 90 0 і cot малого кута, вірні та поправок у них немає. Наприклад, визначити tg 78 0 37хв = 4,967 
а ctg 20 0 13хв = 25,83 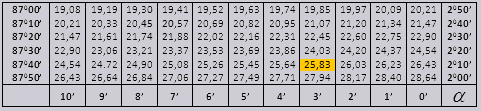
Ну ось ми розглянули основні тригонометричні таблиці. Сподіваємося, ця інформація була для вас вкрай корисною. Свої питання щодо таблиць, якщо вони з'явилися, обов'язково пишіть у коментарях!
Стінові відбійники - відбійна дошка для захисту стін. Перейдіть за посиланням настінні безкаркасні відбійники (http://www.spi-polymer.ru/otboyniki/) і дізнайтесь докладніше.
1. Тригонометричні функціїє елементарними функціями, аргументом яких є кут. За допомогою тригонометричних функцій описуються співвідношення між сторонами та гострими кутами у прямокутному трикутнику. Області застосування тригонометричних функцій надзвичайно різноманітні. Так, наприклад, будь-які періодичні процеси можна подати у вигляді суми тригонометричних функцій (ряду Фур'є). Дані функції часто з'являються під час вирішення диференціальних і функціональних рівнянь.
2. До тригонометричних функцій відносяться такі 6 функцій: синус, косинус, тангенс,котангенс, секансі косеканс. Для кожної із зазначених функцій існує зворотна тригонометрична функція.
3. Геометричне визначення тригонометричних функцій зручно ввести за допомогою одиничного кола. На наведеному нижче малюнку зображено коло радіусом r=1. На колі позначено точку M(x,y). Кут між радіус-вектором OM та позитивним напрямом осі Ox дорівнює α.
4. Сінусомкута називається відношення ординати y точки M(x,y) до радіуса r:
sinα=y/r.
Оскільки r=1, синус дорівнює ординаті точки M(x,y).
5. Косинусомкута α називається відношення абсциси x точки M(x,y) до радіуса r:
cosα=x/r
6. Тангенсомкута α називається відношення ординати y точки M(x,y) до ee абсцис x:
tanα=y/x,x≠0
7. Котангенсомкута α називається відношення абсциси x точки M(x,y) до її ординати y:
cotα=x/y,y≠0
8. Секанскута α - це відношення радіуса r до абсциси x точки M(x, y):
secα=r/x=1/x,x≠0
9. Косеканскута α - це відношення радіуса r до ординати y точки M(x, y):
cscα=r/y=1/y,y≠0
10. У одиничному колі проекції x, y точки M(x,y) та радіус r утворюють прямокутний трикутник, у якому x,y є катетами, а r – гіпотенузою. Тому, наведені вище визначення тригонометричних функцій у додатку до прямокутного трикутника формулюються таким чином:
Сінусомкута називається відношення протилежного катета до гіпотенузи.
Косинусомкута називається відношення прилеглого катета до гіпотенузи.
Тангенсомкута α називається протилежного катета до прилеглого.
Котангенсомкута α називається прилеглого катета до протилежного.
Секанскута α є відношенням гіпотенузи до прилеглого катету.
Косеканскута α є відношенням гіпотенузи до протилежного катету.
11. Графік функції синус
y=sinx, область визначення: x∈R, область значень: −1≤sinx≤1
12. Графік функції косинус
y=cosx, область визначення: x∈R, область значень: −1≤cosx≤1
13. Графік функції тангенс 14. Графік функції котангенс 15. Графік функції секанс
y=tanx, область визначення: x∈R,x≠(2k+1)π/2, область значень: −∞ 
y=cotx, область визначення: x∈R,x≠kπ, область значень: −∞ 
y=secx, область визначення: x∈R,x≠(2k+1)π/2, область значень:secx∈(−∞,−1]∪∪)




