Logarithmische Ungleichungen mit unterschiedlichen Basen, Lösungsbeispiele. Alles über logarithmische Ungleichungen. Analyse von Beispielen

Einführung

Logarithmen wurden erfunden, um Berechnungen zu beschleunigen und zu vereinfachen. Die Idee eines Logarithmus, also die Idee, Zahlen als Potenzen derselben Basis auszudrücken, stammt von Mikhail Stiefel. Aber zu Stiefels Zeiten war die Mathematik noch nicht so weit entwickelt und die Idee des Logarithmus war noch nicht entwickelt. Logarithmen wurden später gleichzeitig und unabhängig voneinander vom schottischen Wissenschaftler John Napier (1550–1617) erfunden, und der Schweizer Jobst Burgi (1552–1632) veröffentlichte das Werk 1614 als Erster. Unter dem Titel „Beschreibung einer erstaunlichen Logarithmentabelle“ wurde Napiers Logarithmentheorie in einem ziemlich vollständigen Band dargelegt, die Methode zur Berechnung von Logarithmen wurde als die einfachste angegeben, daher waren Napiers Verdienste bei der Erfindung der Logarithmen größer als die von Bürgi . Burgi arbeitete zur gleichen Zeit wie Napier an den Tabellen, hielt sie jedoch lange Zeit geheim und veröffentlichte sie erst 1620. Napier beherrschte die Idee des Logarithmus um 1594. obwohl die Tabellen erst 20 Jahre später veröffentlicht wurden. Zuerst nannte er seine Logarithmen „künstliche Zahlen“ und schlug erst dann vor, diese „künstlichen Zahlen“ in einem Wort „Logarithmus“ zu nennen, was aus dem Griechischen übersetzt „korrelierte Zahlen“ bedeutet, eine aus einer arithmetischen Folge und die andere aus a speziell dafür ausgewählter geometrischer Verlauf. Die ersten Tabellen in russischer Sprache wurden 1703 veröffentlicht. unter Beteiligung eines wunderbaren Lehrers des 18. Jahrhunderts. L. F. Magnitsky. Die Werke des St. Petersburger Akademikers Leonhard Euler waren für die Entwicklung der Logarithmentheorie von großer Bedeutung. Er war der erste, der Logarithmen als die Umkehrung der Potenzierung betrachtete; er führte die Begriffe „Logarithmusbasis“ und „Mantisse“ ein. Briggs stellte Logarithmentabellen mit der Basis 10 zusammen. Dezimaltabellen sind ihrer Theorie nach praktischer einfacher als die von Napiers Logarithmen. Daher werden dezimale Logarithmen manchmal auch Briggs-Logarithmen genannt. Der Begriff „Charakterisierung“ wurde von Briggs eingeführt.

In jenen fernen Zeiten, als die Weisen zum ersten Mal über Gleichheiten mit unbekannten Mengen nachzudenken begannen, gab es wahrscheinlich weder Münzen noch Geldbörsen. Es gab aber auch Haufen sowie Töpfe und Körbe, die sich perfekt als Lagerräume eigneten, in denen eine unbekannte Anzahl von Gegenständen aufbewahrt werden konnte. In den antiken mathematischen Problemen Mesopotamiens, Indiens, Chinas und Griechenlands drückten unbekannte Größen die Anzahl der Pfauen im Garten, die Anzahl der Bullen in der Herde und die Gesamtheit der Dinge aus, die bei der Aufteilung des Eigentums berücksichtigt wurden. In das Geheimwissen eingeweihte Schriftgelehrte, Beamte und Priester, die in der Rechnungslegungswissenschaft gut ausgebildet waren, bewältigten solche Aufgaben recht erfolgreich.

Quellen, die uns erreicht haben, weisen darauf hin, dass antike Wissenschaftler über einige allgemeine Techniken zur Lösung von Problemen mit unbekannten Größen verfügten. Allerdings enthält keine einzige Papyrus- oder Tontafel eine Beschreibung dieser Techniken. Nur gelegentlich ergänzten die Autoren ihre numerischen Berechnungen mit knappen Kommentaren wie: „Schau mal!“, „Mach das!“, „Du hast das Richtige gefunden.“ Eine Ausnahme bildet in diesem Sinne die „Arithmetik“ des griechischen Mathematikers Diophantus von Alexandria (III. Jahrhundert) – eine Sammlung von Problemen zum Aufstellen von Gleichungen mit einer systematischen Darstellung ihrer Lösungen.

Das erste Handbuch zur Problemlösung, das weithin bekannt wurde, war jedoch das Werk des Bagdader Wissenschaftlers aus dem 9. Jahrhundert. Muhammad bin Musa al-Khwarizmi. Das Wort „al-jabr“ aus dem arabischen Namen dieser Abhandlung – „Kitab al-jaber wal-mukabala“ („Buch der Wiederherstellung und Opposition“) – verwandelte sich im Laufe der Zeit in das bekannte Wort „Algebra“ und das Werk von al-Khwarizmi selbst diente als Ausgangspunkt für die Entwicklung der Wissenschaft des Lösens von Gleichungen.

Logarithmische Gleichungen und Ungleichungen

1. Logarithmische Gleichungen

Eine Gleichung, die eine Unbekannte unter dem Logarithmuszeichen oder an ihrer Basis enthält, wird logarithmische Gleichung genannt.

Die einfachste logarithmische Gleichung ist eine Gleichung der Form

Protokoll A X = B . (1)

Aussage 1. Wenn A > 0, A≠ 1, Gleichung (1) für jede reelle Zahl B hat eine einzigartige Lösung X = ein b .

Beispiel 1. Lösen Sie die Gleichungen:

a)log 2 X= 3, b) log 3 X= -1, c)

Lösung. Mit Aussage 1 erhalten wir a) X= 2 3 oder X= 8; B) X= 3 -1 oder X= 1 / 3 ; C)

Lassen Sie uns die grundlegenden Eigenschaften des Logarithmus vorstellen.

P1. Grundlegende logarithmische Identität:

Wo A > 0, A≠ 1 und B > 0.

P2. Der Logarithmus des Produkts positiver Faktoren ist gleich der Summe der Logarithmen dieser Faktoren:

Protokoll A N 1 · N 2 = log A N 1 + Protokoll A N 2 (A > 0, A ≠ 1, N 1 > 0, N 2 > 0).

Kommentar. Wenn N 1 · N 2 > 0, dann nimmt die Eigenschaft P2 die Form an

Protokoll A N 1 · N 2 = log A |N 1 | +log A |N 2 | (A > 0, A ≠ 1, N 1 · N 2 > 0).

P3. Der Logarithmus des Quotienten zweier positiver Zahlen ist gleich der Differenz zwischen den Logarithmen des Dividenden und des Divisors

Kommentar. Wenn

P4. Der Logarithmus der Potenz einer positiven Zahl ist gleich dem Produkt aus dem Exponenten und dem Logarithmus dieser Zahl:

Protokoll A N k = k Protokoll A N (A > 0, A ≠ 1, N > 0).

Kommentar. Wenn k- gerade Zahl ( k = 2S), Das

Protokoll A N 2S = 2S Protokoll A |N | (A > 0, A ≠ 1, N ≠ 0).

P5. Formel für den Umzug zu einer anderen Basis:

insbesondere wenn N = B, bekommen wir

Mit den Eigenschaften P4 und P5 lassen sich leicht die folgenden Eigenschaften ermitteln

und wenn in (5) C- gerade Zahl ( C = 2N), stattfindet

Lassen Sie uns die Haupteigenschaften der logarithmischen Funktion auflisten F (X) = log A X :

1. Der Definitionsbereich einer logarithmischen Funktion ist die Menge der positiven Zahlen.

2. Der Wertebereich der logarithmischen Funktion ist die Menge der reellen Zahlen.

3. Wann A> 1 logarithmische Funktion ist streng wachsend (0< X 1 < X 2log A X 1 < logA X 2) und bei 0< A < 1, - строго убывает (0 < X 1 < X 2log A X 1 > Protokoll A X 2).

4.log A 1 = 0 und log A A = 1 (A > 0, A ≠ 1).

5. Wenn A> 1, dann ist die logarithmische Funktion negativ, wenn X(0;1) und positiv bei X(1;+∞), und wenn 0< A < 1, то логарифмическая функция положительна при X (0;1) und negativ bei X (1;+∞).

6. Wenn A> 1, dann ist die logarithmische Funktion konvex nach oben, und wenn A(0;1) - konvex nach unten.

Die folgenden Aussagen (siehe zum Beispiel) werden beim Lösen logarithmischer Gleichungen verwendet.

Unter der ganzen Vielfalt logarithmischer Ungleichungen werden Ungleichungen mit variabler Basis gesondert untersucht. Sie werden mit einer speziellen Formel gelöst, die aus irgendeinem Grund in der Schule selten gelehrt wird:

log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0

Anstelle des Kontrollkästchens „∨“ können Sie ein beliebiges Ungleichheitszeichen setzen: mehr oder weniger. Die Hauptsache ist, dass in beiden Ungleichungen die Vorzeichen gleich sind.

Auf diese Weise beseitigen wir Logarithmen und reduzieren das Problem auf eine rationale Ungleichung. Letzteres ist viel einfacher zu lösen, aber wenn Logarithmen verworfen werden, können zusätzliche Wurzeln entstehen. Um sie abzuschneiden, reicht es aus, den Bereich akzeptabler Werte zu ermitteln. Wenn Sie die ODZ eines Logarithmus vergessen haben, empfehle ich dringend, sie zu wiederholen – siehe „Was ist ein Logarithmus“.

Alles, was mit dem Bereich akzeptabler Werte zusammenhängt, muss separat ausgeschrieben und gelöst werden:

f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.

Diese vier Ungleichungen bilden ein System und müssen gleichzeitig erfüllt sein. Wenn der Bereich akzeptabler Werte gefunden ist, müssen Sie ihn nur noch mit der Lösung der rationalen Ungleichung schneiden – und schon ist die Antwort fertig.

Aufgabe. Lösen Sie die Ungleichung:

Schreiben wir zunächst die ODZ des Logarithmus auf:

Die ersten beiden Ungleichungen werden automatisch erfüllt, die letzte muss jedoch ausgeschrieben werden. Da das Quadrat einer Zahl genau dann Null ist, wenn die Zahl selbst Null ist, gilt:

x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.

Es stellt sich heraus, dass die ODZ des Logarithmus alle Zahlen außer Null sind: x ∈ (−∞ 0)∪(0; +∞). Jetzt lösen wir die Hauptungleichung:

Wir machen den Übergang von der logarithmischen zur rationalen Ungleichung. Die ursprüngliche Ungleichung hat ein „Kleiner-als“-Zeichen, was bedeutet, dass die resultierende Ungleichung auch ein „Kleiner-als“-Zeichen haben muss. Wir haben:

(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x ) (3 + x ) x 2< 0.

Die Nullstellen dieses Ausdrucks sind: x = 3; x = −3; x = 0. Darüber hinaus ist x = 0 eine Wurzel der zweiten Multiplizität, was bedeutet, dass sich das Vorzeichen der Funktion beim Durchlaufen nicht ändert. Wir haben:

Wir erhalten x ∈ (−∞ −3)∪(3; +∞). Diese Menge ist vollständig in der ODZ des Logarithmus enthalten, was bedeutet, dass dies die Antwort ist.

Logarithmische Ungleichungen umwandeln

Oftmals unterscheidet sich die ursprüngliche Ungleichung von der oben genannten. Dies lässt sich leicht mit den Standardregeln für die Arbeit mit Logarithmen korrigieren – siehe „Grundlegende Eigenschaften von Logarithmen“. Nämlich:

1. Jede Zahl kann als Logarithmus mit einer bestimmten Basis dargestellt werden;
2. Die Summe und Differenz von Logarithmen gleicher Basis kann durch einen Logarithmus ersetzt werden.

Unabhängig davon möchte ich Sie an den Bereich akzeptabler Werte erinnern. Da es in der ursprünglichen Ungleichung mehrere Logarithmen geben kann, ist es erforderlich, die VA für jeden von ihnen zu ermitteln. Das allgemeine Schema zur Lösung logarithmischer Ungleichungen lautet daher wie folgt:

1. Finden Sie die VA jedes in der Ungleichung enthaltenen Logarithmus.
2. Reduzieren Sie die Ungleichung auf eine Standardungleichung, indem Sie die Formeln zum Addieren und Subtrahieren von Logarithmen verwenden.
3. Lösen Sie die resultierende Ungleichung nach dem oben angegebenen Schema.

Aufgabe. Lösen Sie die Ungleichung:

Finden wir den Definitionsbereich (DO) des ersten Logarithmus:

Wir lösen mit der Intervallmethode. Finden der Nullstellen des Zählers:

3x − 2 = 0;
x = 2/3.

Dann - die Nullen des Nenners:

x − 1 = 0;
x = 1.

Wir markieren Nullen und Vorzeichen auf dem Koordinatenpfeil:

Wir erhalten x ∈ (−∞ 2/3)∪(1; +∞). Der zweite Logarithmus hat die gleiche VA. Wenn Sie mir nicht glauben, können Sie es überprüfen. Jetzt transformieren wir den zweiten Logarithmus so, dass die Basis zwei ist:

Wie Sie sehen, wurden die Dreien an der Basis und vor dem Logarithmus reduziert. Wir haben zwei Logarithmen mit derselben Basis. Addieren wir sie:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .

Wir haben die logarithmische Standardungleichung erhalten. Mit der Formel werden wir Logarithmen los. Da die ursprüngliche Ungleichung ein „Kleiner-als“-Zeichen enthält, muss der resultierende rationale Ausdruck ebenfalls kleiner als Null sein. Wir haben:

(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).

Wir haben zwei Sets bekommen:

1. ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
2. Kandidatenantwort: x ∈ (−1; 3).

Es bleibt noch, diese Mengen zu schneiden – wir erhalten die eigentliche Antwort:

Uns interessiert der Schnittpunkt von Mengen, daher wählen wir Intervalle aus, die auf beiden Pfeilen schattiert sind. Wir erhalten x ∈ (−1; 2/3)∪(1; 3) – alle Punkte sind punktiert.

Glauben Sie, dass bis zum Einheitlichen Staatsexamen noch Zeit ist und Sie Zeit haben werden, sich vorzubereiten? Vielleicht ist das so. Aber je früher ein Student mit der Vorbereitung beginnt, desto erfolgreicher besteht er die Prüfungen. Heute haben wir beschlossen, den logarithmischen Ungleichungen einen Artikel zu widmen. Dies ist eine der Aufgaben und bietet die Möglichkeit, zusätzliche Credits zu erhalten.

Wissen Sie schon, was ein Logarithmus ist? Das hoffen wir wirklich. Aber auch wenn Sie auf diese Frage keine Antwort haben, ist das kein Problem. Es ist sehr einfach zu verstehen, was ein Logarithmus ist.

Warum 4? Sie müssen die Zahl 3 auf diese Potenz erhöhen, um 81 zu erhalten. Sobald Sie das Prinzip verstanden haben, können Sie mit komplexeren Berechnungen fortfahren.

Sie haben vor ein paar Jahren Ungleichheiten erlebt. Und seitdem begegnet man ihnen ständig in der Mathematik. Wenn Sie Probleme beim Lösen von Ungleichungen haben, lesen Sie den entsprechenden Abschnitt.
Nachdem wir uns nun mit den Konzepten im Einzelnen vertraut gemacht haben, gehen wir dazu über, sie im Allgemeinen zu betrachten.

Die einfachste logarithmische Ungleichung.

Die einfachsten logarithmischen Ungleichungen sind nicht auf dieses Beispiel beschränkt; es gibt noch drei weitere, nur mit unterschiedlichen Vorzeichen. Warum ist das notwendig? Um besser zu verstehen, wie man Ungleichungen mit Logarithmen löst. Lassen Sie uns nun ein anwendbareres Beispiel geben, das immer noch recht einfach ist. Wir werden komplexe logarithmische Ungleichungen für später aufheben.

Wie kann man das lösen? Alles beginnt mit ODZ. Es lohnt sich, mehr darüber zu wissen, wenn Sie Ungleichungen immer einfach lösen möchten.

Was ist ODZ? ODZ für logarithmische Ungleichungen

Die Abkürzung steht für den Bereich akzeptabler Werte. Diese Formulierung kommt häufig in Aufgaben für das Einheitliche Staatsexamen vor. ODZ wird Ihnen nicht nur bei logarithmischen Ungleichungen nützlich sein.

Schauen Sie sich noch einmal das obige Beispiel an. Wir werden die darauf basierende ODZ betrachten, damit Sie das Prinzip verstehen und die Lösung logarithmischer Ungleichungen keine Fragen aufwirft. Aus der Definition eines Logarithmus folgt, dass 2x+4 größer als Null sein muss. In unserem Fall bedeutet dies Folgendes.

Diese Zahl muss per Definition positiv sein. Lösen Sie die oben dargestellte Ungleichung. Dies kann sogar mündlich erfolgen; hier ist klar, dass X nicht kleiner als 2 sein kann. Die Lösung der Ungleichung wird die Definition des Bereichs akzeptabler Werte sein.
Kommen wir nun zur Lösung der einfachsten logarithmischen Ungleichung.

Wir verwerfen die Logarithmen selbst auf beiden Seiten der Ungleichung. Was bleibt uns als Ergebnis übrig? Einfache Ungleichheit.

Es ist nicht schwer zu lösen. X muss größer als -0,5 sein. Nun kombinieren wir die beiden erhaltenen Werte zu einem System. Daher,

Dies ist der Bereich akzeptabler Werte für die betrachtete logarithmische Ungleichung.

Warum brauchen wir überhaupt ODZ? Dies ist eine Gelegenheit, falsche und unmögliche Antworten auszusortieren. Wenn die Antwort nicht im Bereich akzeptabler Werte liegt, ergibt die Antwort einfach keinen Sinn. Daran sollte man sich noch lange erinnern, da im Einheitlichen Staatsexamen häufig nach ODZ gesucht werden muss und es sich dabei nicht nur um logarithmische Ungleichungen handelt.

Algorithmus zur Lösung logarithmischer Ungleichungen

Die Lösung besteht aus mehreren Schritten. Zunächst müssen Sie den Bereich akzeptabler Werte ermitteln. In der ODZ wird es zwei Werte geben, die wir oben besprochen haben. Als nächstes müssen Sie die Ungleichung selbst lösen. Die Lösungsmethoden sind wie folgt:

• Multiplikator-Ersetzungsmethode;
• Zersetzung;
• Rationalisierungsmethode.

Je nach Situation lohnt es sich, eine der oben genannten Methoden anzuwenden. Kommen wir direkt zur Lösung. Lassen Sie uns die beliebteste Methode vorstellen, die in fast allen Fällen zur Lösung von Aufgaben des Einheitlichen Staatsexamens geeignet ist. Als nächstes werden wir uns die Zerlegungsmethode ansehen. Es kann hilfreich sein, wenn Sie auf eine besonders knifflige Ungleichung stoßen. Also ein Algorithmus zur Lösung der logarithmischen Ungleichung.

Beispiele für Lösungen :

Nicht umsonst haben wir genau diese Ungleichung angenommen! Achten Sie auf die Basis. Denken Sie daran: Wenn er größer als eins ist, bleibt das Vorzeichen beim Ermitteln des Bereichs akzeptabler Werte gleich; Andernfalls müssen Sie das Ungleichheitszeichen ändern.

Als Ergebnis erhalten wir die Ungleichung:

Jetzt reduzieren wir die linke Seite auf die Form der Gleichung gleich Null. Anstelle des „kleiner als“-Zeichens setzen wir „gleich“ und lösen die Gleichung. Somit finden wir die ODZ. Wir hoffen, dass Sie keine Probleme haben werden, eine solch einfache Gleichung zu lösen. Die Antworten sind -4 und -2. Das ist noch nicht alles. Sie müssen diese Punkte in der Grafik anzeigen, indem Sie „+“ und „-“ platzieren. Was muss hierfür getan werden? Setzen Sie die Zahlen aus den Intervallen in den Ausdruck ein. Bei positiven Werten setzen wir dort „+“.

Antwort: x kann nicht größer als -4 und kleiner als -2 sein.

Wir haben den Bereich akzeptabler Werte nur für die linke Seite gefunden, jetzt müssen wir den Bereich akzeptabler Werte für die rechte Seite ermitteln. Das ist viel einfacher. Antwort: -2. Wir schneiden beide resultierenden Bereiche.

Und erst jetzt beginnen wir, uns mit der Ungleichheit selbst zu befassen.

Vereinfachen wir es so weit wie möglich, damit es einfacher zu lösen ist.

Wir verwenden in der Lösung erneut die Intervallmethode. Lassen Sie uns die Berechnungen überspringen; aus dem vorherigen Beispiel ist bereits alles klar. Antwort.

Diese Methode ist jedoch geeignet, wenn die logarithmische Ungleichung die gleichen Basen hat.

Das Lösen logarithmischer Gleichungen und Ungleichungen mit unterschiedlichen Basen erfordert zunächst eine Reduktion auf die gleiche Basis. Als nächstes verwenden Sie die oben beschriebene Methode. Aber es gibt einen komplizierteren Fall. Betrachten wir eine der komplexesten Arten logarithmischer Ungleichungen.

Logarithmische Ungleichungen mit variabler Basis

Wie löst man Ungleichungen mit solchen Merkmalen? Ja, und solche Leute können im Einheitlichen Staatsexamen gefunden werden. Die Lösung von Ungleichheiten auf die folgende Weise wird sich auch positiv auf Ihren Bildungsprozess auswirken. Schauen wir uns das Problem im Detail an. Verwerfen wir die Theorie und gehen direkt zur Praxis über. Um logarithmische Ungleichungen zu lösen, genügt es, sich einmal mit dem Beispiel vertraut zu machen.

Um eine logarithmische Ungleichung der dargestellten Form zu lösen, ist es notwendig, die rechte Seite auf einen Logarithmus mit derselben Basis zu reduzieren. Das Prinzip ähnelt äquivalenten Übergängen. Infolgedessen wird die Ungleichung so aussehen.

Eigentlich bleibt nur noch die Schaffung eines Systems von Ungleichungen ohne Logarithmen. Mit der Rationalisierungsmethode gelangen wir zu einem äquivalenten Ungleichungssystem. Sie werden die Regel selbst verstehen, wenn Sie die entsprechenden Werte ersetzen und deren Änderungen verfolgen. Das System weist die folgenden Ungleichungen auf.

Wenn Sie beim Lösen von Ungleichungen die Rationalisierungsmethode verwenden, müssen Sie Folgendes beachten: Eins muss von der Basis subtrahiert werden, x wird per Definition des Logarithmus von beiden Seiten der Ungleichung (rechts von links) subtrahiert, zwei Ausdrücke werden multipliziert und unter das ursprüngliche Vorzeichen in Bezug auf Null gesetzt.

Die weitere Lösung erfolgt mit der Intervallmethode, hier ist alles einfach. Es ist wichtig, dass Sie die Unterschiede in den Lösungsmethoden verstehen, dann wird alles reibungslos funktionieren.

Bei logarithmischen Ungleichungen gibt es viele Nuancen. Die einfachsten davon sind recht einfach zu lösen. Wie können Sie jedes davon ohne Probleme lösen? Alle Antworten haben Sie bereits in diesem Artikel erhalten. Jetzt liegt eine lange Übung vor Ihnen. Üben Sie ständig das Lösen verschiedener Aufgaben in der Prüfung und Sie werden in der Lage sein, die höchste Punktzahl zu erreichen. Viel Glück für Ihre schwierige Aufgabe!

Bis zum Bestehen der Einheitlichen Staatsprüfung in Mathematik bleibt immer weniger Zeit. Die Situation spitzt sich zu, die Nerven von Schülern, Eltern, Lehrern und Nachhilfelehrern werden zunehmend strapaziert. Tägliche, ausführliche Mathematikkurse helfen Ihnen, nervöse Anspannungen abzubauen. Denn wie wir wissen, motiviert Sie nichts so positiv und hilft Ihnen, Prüfungen zu bestehen, wie das Vertrauen in Ihre Fähigkeiten und Ihr Wissen. Heute wird Ihnen ein Mathematiklehrer etwas über das Lösen von Systemen logarithmischer und exponentieller Ungleichungen erzählen, Aufgaben, die vielen modernen Gymnasiasten traditionell Schwierigkeiten bereiten.

Um als Nachhilfelehrer für Mathematik zu lernen, wie man C3-Aufgaben aus dem Einheitlichen Staatsexamen in Mathematik löst, empfehle ich Ihnen, die folgenden wichtigen Punkte zu beachten.

1. Bevor Sie mit der Lösung von Systemen logarithmischer und exponentieller Ungleichungen beginnen, müssen Sie lernen, wie Sie jede dieser Arten von Ungleichungen einzeln lösen. Um insbesondere zu verstehen, wie der Bereich akzeptabler Werte liegt, werden äquivalente Transformationen logarithmischer und exponentieller Ausdrücke durchgeführt. Sie können einige der damit verbundenen Geheimnisse verstehen, indem Sie die Artikel „“ und „“ lesen.

2. Gleichzeitig muss man sich darüber im Klaren sein, dass die Lösung eines Systems von Ungleichungen nicht immer darauf hinausläuft, jede Ungleichung einzeln zu lösen und die resultierenden Intervalle zu schneiden. Wenn man die Lösung für eine Ungleichung des Systems kennt, wird die Lösung für die zweite manchmal viel einfacher. Als Nachhilfelehrer für Mathematik, der Schüler auf die Abschlussprüfungen im Format des Einheitlichen Staatsexamens vorbereitet, verrate ich in diesem Artikel einige diesbezügliche Geheimnisse.

3. Es ist notwendig, den Unterschied zwischen Schnittmenge und Vereinigung von Mengen klar zu verstehen. Dies ist eines der wichtigsten mathematischen Kenntnisse, die ein erfahrener professioneller Nachhilfelehrer seinem Schüler von den ersten Unterrichtsstunden an zu vermitteln versucht. Eine visuelle Darstellung des Schnittpunkts und der Vereinigung von Mengen bieten die sogenannten „Euleschen Kreise“.

Schnittmenge von Mengen ist eine Menge, die nur die Elemente enthält, die jede dieser Mengen hat.

Überschneidung

Darstellung des Schnittpunktes von Mengen mittels „Eulescher Kreise“

Erklärungen immer zur Hand. Diana hat ein „Set“ in ihrer Handtasche, bestehend aus ( Stifte, Bleistift, Herrscher, Notizbücher, Kämme). Alice hat ein „Set“ in ihrer Handtasche, bestehend aus ( Notizbuch, Bleistift, Spiegel, Notizbücher, Hühnchen Kiew). Der Schnittpunkt dieser beiden „Mengen“ ist die „Menge“, bestehend aus ( Bleistift, Notizbücher), da sowohl Diana als auch Alice beide dieser „Elemente“ haben.

Wichtig zu beachten! Wenn die Lösung einer Ungleichung ein Intervall ist und die Lösung einer Ungleichung ein Intervall ist, dann lautet die Lösung der Systeme:

ist das Intervall, das ist Überschneidung Originalintervalle. Hier und untenbedeutet eines der Zeichen title="Rendered by QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">!} und darunter - es ist das umgekehrte Vorzeichen.

Vereinigung von Mengen ist eine Menge, die aus allen Elementen der Originalmengen besteht.

Mit anderen Worten, wenn zwei Mengen gegeben sind und dann ihre Vereinigung wird ein Satz der folgenden Form sein:

Darstellung der Mengenvereinigung mittels „Eulescher Kreise“

Erklärungen immer zur Hand. Die Vereinigung der im vorherigen Beispiel genommenen „Mengen“ ist die „Menge“, bestehend aus ( Stifte, Bleistift, Herrscher, Notizbücher, Kämme, Notizbuch, Spiegel, Hühnchen Kiew), da es aus allen Elementen der ursprünglichen „Mengen“ besteht. Eine Klarstellung, die möglicherweise nicht überflüssig ist. Viele kippen enthalten identische Elemente.

Wichtig zu beachten! Wenn die Lösung einer Ungleichung ein Intervall und die Lösung einer Ungleichung ein Intervall ist, dann lautet die Lösung der Grundgesamtheit:

ist das Intervall, das ist Verein Originalintervalle.

Kommen wir direkt zu den Beispielen.

Beispiel 1. Lösen Sie das Ungleichungssystem:

Lösung für Problem C3.

1. Lösen wir zunächst die erste Ungleichung. Mit der Substitution gelangen wir zur Ungleichung:

2. Lösen wir nun die zweite Ungleichung. Der Bereich seiner zulässigen Werte wird durch die Ungleichung bestimmt:

Title="Rendered by QuickLaTeX.com">!}

Im Bereich akzeptabler Werte, unter Berücksichtigung der Tatsache, dass die Basis des Logarithmus title="Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству:!}

Unter Ausschluss von Lösungen, die nicht im Bereich akzeptabler Werte liegen, erhalten wir das Intervall

3. Beantworten System Es wird Ungleichheiten geben Überschneidung

Die resultierenden Intervalle auf der Zahlengeraden. Die Lösung ist ihr Schnittpunkt

Beispiel 2. Lösen Sie das Ungleichungssystem:

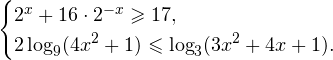
Lösung für Problem C3.

1. Lösen wir zunächst die erste Ungleichung. Multiplizieren Sie beide Teile mit title="Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству:!}

Kommen wir zur umgekehrten Substitution:

2.

Title="Rendered by QuickLaTeX.com">!}

Grafische Darstellung des resultierenden Intervalls. Die Lösung des Systems ist ihre Schnittmenge

Beispiel 3. Lösen Sie das Ungleichungssystem:

Lösung für Problem C3.

1. Lösen wir zunächst die erste Ungleichung. Multiplizieren Sie beide Teile mit title="Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство:!}

Durch Substitution gelangen wir zu folgender Ungleichung:

Kommen wir zur umgekehrten Substitution:

2. Lösen wir nun die zweite Ungleichung. Bestimmen wir zunächst den Bereich der zulässigen Werte dieser Ungleichung:

ql-right-eqno">

Bitte beachten Sie das

Unter Berücksichtigung des Bereichs akzeptabler Werte erhalten wir dann:

3. Wir finden eine allgemeine Lösung für die Ungleichungen. Der Vergleich der erhaltenen irrationalen Werte von Knotenpunkten ist in diesem Beispiel keineswegs eine triviale Aufgabe. Sie können dies wie folgt tun. Weil

Title="Rendered by QuickLaTeX.com">!}

Das und die endgültige Antwort an das System sieht so aus:

Beispiel 4. Lösen Sie das Ungleichungssystem:

Lösung des Problems C3.

1. Lösen wir zunächst die zweite Ungleichung:

2. Die erste Ungleichung des ursprünglichen Systems ist eine logarithmische Ungleichung mit variabler Basis. Eine bequeme Möglichkeit, solche Ungleichungen zu lösen, wird im Artikel „Komplexe logarithmische Ungleichungen“ beschrieben. Sie basiert auf einer einfachen Formel:

Das Vorzeichen kann durch ein beliebiges Ungleichheitszeichen ersetzt werden, Hauptsache es ist in beiden Fällen dasselbe. Die Verwendung dieser Formel vereinfacht die Lösung der Ungleichung erheblich:

Lassen Sie uns nun den Bereich akzeptabler Werte dieser Ungleichung bestimmen. Es wird durch das folgende System festgelegt:

Title="Rendered by QuickLaTeX.com">!}

Title="Rendered by QuickLaTeX.com">!}

Es ist leicht zu erkennen, dass dieses Intervall gleichzeitig auch eine Lösung für unsere Ungleichung sein wird.

3. Die endgültige Antwort auf das Original Systeme Es wird Ungleichheiten geben Überschneidung die resultierenden Intervalle, das heißt

Beispiel 5. Lösen Sie das Ungleichungssystem:

Lösung zu Aufgabe C3.

1. Lösen wir zunächst die erste Ungleichung. Wir verwenden Substitution. Wir gehen zu der folgenden quadratischen Ungleichung über:

2. Lösen wir nun die zweite Ungleichung. Der Bereich seiner zulässigen Werte wird vom System bestimmt:

Title="Rendered by QuickLaTeX.com">!}

Diese Ungleichung entspricht dem folgenden gemischten System:

Im Bereich akzeptabler Werte, also mit title="Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе:!}

Unter Berücksichtigung des Bereichs akzeptabler Werte erhalten wir:

3. Die endgültige Entscheidung des Originals Systeme Ist

Lösung für Problem C3.

1. Lösen wir zunächst die erste Ungleichung. Durch äquivalente Transformationen bringen wir es auf die Form:

2. Lösen wir nun die zweite Ungleichung. Der Bereich seiner gültigen Werte wird durch das Intervall bestimmt: title="Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству:!}

Diese Antwort gehört vollständig zum Bereich akzeptabler Ungleichheitswerte.

3. Indem wir die in den vorherigen Absätzen erhaltenen Intervalle schneiden, erhalten wir die endgültige Antwort auf das Ungleichungssystem:

Heute haben wir Systeme logarithmischer und exponentieller Ungleichungen gelöst. Aufgaben dieser Art wurden im laufenden Studienjahr in Probeversionen des Einheitlichen Staatsexamens in Mathematik angeboten. Als Mathematiklehrer mit Erfahrung in der Vorbereitung auf das Einheitliche Staatsexamen kann ich jedoch sagen, dass dies keineswegs bedeutet, dass es im Juni in den realen Versionen des Einheitlichen Staatsexamens in Mathematik ähnliche Aufgaben geben wird.

Lassen Sie mich eine Warnung aussprechen, die sich in erster Linie an Nachhilfelehrer und Schullehrer richtet, die Oberstufenschüler auf das Einheitliche Staatsexamen in Mathematik vorbereiten. Es ist sehr gefährlich, Schüler strikt nach vorgegebenen Themen auf eine Prüfung vorzubereiten, da in diesem Fall die Gefahr besteht, dass sie bereits bei geringfügiger Änderung des zuvor genannten Aufgabenformats völlig durchfällt. Die Mathematikausbildung muss abgeschlossen sein. Liebe Kolleginnen und Kollegen, bitte vergleichen Sie Ihre Schüler nicht mit Robotern, indem sie ihnen die Lösung einer bestimmten Art von Problem beibringen. Schließlich gibt es nichts Schlimmeres als die Formalisierung des menschlichen Denkens.

Viel Glück und kreativen Erfolg an alle!

Sergej Walerjewitsch

Wenn Sie es versuchen, gibt es zwei Möglichkeiten: Es wird funktionieren oder es wird nicht funktionieren. Wenn Sie es nicht versuchen, gibt es nur einen.
© Volksweisheit