Логаритмични неравенства с различни основи, примери за решения. Всичко за логаритмичните неравенства. Анализ на примери

Въведение

Логаритмите са измислени, за да ускорят и опростят изчисленията. Идеята за логаритъм, тоест идеята за изразяване на числата като мощности на една и съща основа, принадлежи на Михаил Щифел. Но по времето на Щифел математиката не беше толкова развита и идеята за логаритъма не беше развита. По-късно логаритмите са изобретени едновременно и независимо един от друг от шотландския учен Джон Напиер (1550-1617) и швейцареца Йобст Бурги (1552-1632) е първият, който публикува работата си през 1614 г. под заглавието „Описание на невероятна таблица с логаритми“ теорията на Напиер за логаритмите беше дадена в доста пълен обем, методът за изчисляване на логаритми беше даден най-простият, следователно заслугите на Напиер в изобретяването на логаритми бяха по-големи от тези на Бюрги. Бурги работи върху таблиците едновременно с Напиер, но ги пази в тайна дълго време и ги публикува едва през 1620 г. Напиер усвоява идеята за логаритъма около 1594 г. въпреки че таблиците са публикувани 20 години по-късно. Отначало той нарече своите логаритми „изкуствени числа“ и едва след това предложи тези „изкуствени числа“ да се наричат с една дума „логаритъм“, което в превод от гръцки означава „корелирани числа“, взети едно от аритметична прогресия, а другото от геометрична прогресия, специално подбрана за него. Първите таблици на руски език са публикувани през 1703 г. с участието на прекрасен учител от 18 век. Л. Ф. Магнитски. Трудовете на петербургския академик Леонхард Ойлер са от голямо значение за развитието на теорията на логаритмите. Той е първият, който разглежда логаритмите като обратна на повишаването на степен; той въвежда термините „логаритмична основа“ и „мантиса“, съставена от логаритми с основа 10. Десетичните таблици са по-удобни за практическа употреба, тяхната теория е. по-проста от тази на логаритмите на Напиер. Следователно десетичните логаритми понякога се наричат логаритми на Бригс. Терминът "охарактеризиране" е въведен от Бригс.

В онези далечни времена, когато мъдреците за първи път започнаха да мислят за равенства, съдържащи неизвестни количества, вероятно не е имало монети или портфейли. Но имаше купища, както и саксии и кошници, които бяха идеални за ролята на тайници за съхранение, които можеха да поберат неизвестен брой предмети. В древните математически задачи на Месопотамия, Индия, Китай, Гърция неизвестните величини изразяват броя на пауните в градината, броя на биковете в стадото и съвкупността от неща, взети предвид при разделянето на имуществото. Писари, служители и свещеници, посветени в тайни знания, добре обучени в науката за сметките, се справяха доста успешно с подобни задачи.

Достигналите до нас източници показват, че древните учени са имали някои общи техники за решаване на проблеми с неизвестни величини. Въпреки това нито един папирус или глинена плочка не съдържа описание на тези техники. Авторите само от време на време снабдяваха числените си изчисления с оскъдни коментари като: „Вижте!“, „Направете това!“, „Намерихте правилния“. В този смисъл изключение прави „Аритметиката” на гръцкия математик Диофант от Александрия (III в.) – сборник от задачи за съставяне на уравнения със систематично представяне на техните решения.

Но първото ръководство за решаване на проблеми, което стана широко известно, беше дело на багдадския учен от 9 век. Мохамед бин Муса ал-Хорезми. Думата "ал-джабр" от арабското име на този трактат - "Китаб ал-джабер уол-мукабала" ("Книга на възстановяването и противопоставянето") - с течение на времето се превърна в добре познатата дума "алгебра", а ал- Самата работа на Хорезми послужи като отправна точка в развитието на науката за решаване на уравнения.

Логаритмични уравнения и неравенства

1. Логаритмични уравнения

Уравнение, което съдържа неизвестно под знака на логаритъма или в основата си, се нарича логаритмично уравнение.

Най-простото логаритмично уравнение е уравнение от формата

дневник а х = b . (1)

Твърдение 1. Ако а > 0, а≠ 1, уравнение (1) за всяко реално bима уникално решение х = а б .

Пример 1. Решете уравненията:

а) дневник 2 х= 3, b) log 3 х= -1, в)

Решение. Използвайки твърдение 1, получаваме а) х= 2 3 или х= 8; б) х= 3 -1 или х= 1/3; ° С)

или х = 1.

Нека представим основните свойства на логаритъма.

P1. Основна логаритмична идентичност:

Където а > 0, а≠ 1 и b > 0.

P2. Логаритъмът на произведението на положителните фактори е равен на сумата от логаритмите на тези фактори:

дневник а н 1 · н 2 = дневник а н 1 + дневник а н 2 (а > 0, а ≠ 1, н 1 > 0, н 2 > 0).

Коментирайте. Ако н 1 · н 2 > 0, тогава свойството P2 приема формата

дневник а н 1 · н 2 = дневник а |н 1 | + дневник а |н 2 | (а > 0, а ≠ 1, н 1 · н 2 > 0).

P3. Логаритъмът от частното на две положителни числа е равен на разликата между логаритмите на делителя и делителя

(а > 0, а ≠ 1, н 1 > 0, н 2 > 0).

Коментирайте. Ако

, (което е еквивалентно н 1 н 2 > 0), тогава свойството P3 приема формата

(а > 0, а ≠ 1, н 1 н 2 > 0).

P4. Логаритъмът на степента на положително число е равен на произведението на степента и логаритъма на това число:

дневник а н к = кдневник а н (а > 0, а ≠ 1, н > 0).

Коментирайте. Ако к- четен брой ( к = 2с), Че

дневник а н 2с = 2сдневник а |н | (а > 0, а ≠ 1, н ≠ 0).

P5. Формула за преместване в друга база:

(а > 0, а ≠ 1, b > 0, b ≠ 1, н > 0),

особено ако н = b, получаваме

(а > 0, а ≠ 1, b > 0, b ≠ 1). (2)

Използвайки свойства P4 и P5, е лесно да се получат следните свойства

(а > 0, а ≠ 1, b > 0, ° С ≠ 0), (3) (а > 0, а ≠ 1, b > 0, ° С ≠ 0), (4)

(а > 0, а ≠ 1, b > 0, ° С ≠ 0), (5)

и ако в (5) ° С- четен брой ( ° С = 2н), възниква

(b > 0, а ≠ 0, |а | ≠ 1). (6)

Нека изброим основните свойства на логаритмичната функция f (х) = дневник а х :

1. Областта на дефиниране на логаритмична функция е множеството от положителни числа.

2. Диапазонът от стойности на логаритмичната функция е набор от реални числа.

3. Кога а> 1 логаритмична функция е строго нарастваща (0< х 1 < х 2log а х 1 < logа х 2) и на 0< а < 1, - строго убывает (0 < х 1 < х 2log а х 1 > дневник а х 2).

4.дневник а 1 = 0 и log а а = 1 (а > 0, а ≠ 1).

5. Ако а> 1, тогава логаритмичната функция е отрицателна, когато х(0;1) и положителен при х(1;+∞), и ако 0< а < 1, то логарифмическая функция положительна при х (0;1) и отрицателен при х (1;+∞).

6. Ако а> 1, тогава логаритмичната функция е изпъкнала нагоре и ако а(0;1) - изпъкнал надолу.

Следните твърдения (вижте например) се използват при решаване на логаритмични уравнения.

Сред цялото разнообразие от логаритмични неравенства отделно се изучават неравенствата с променлива основа. Те се решават с помощта на специална формула, която по някаква причина рядко се преподава в училище:

log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0

Вместо квадратчето за отметка „∨“ можете да поставите произволен знак за неравенство: повече или по-малко. Основното е, че и в двете неравенства знаците са еднакви.

По този начин се отърваваме от логаритмите и свеждаме проблема до рационално неравенство. Последното е много по-лесно за решаване, но при изхвърляне на логаритми може да се появят допълнителни корени. За да ги отрежете, достатъчно е да намерите диапазона от приемливи стойности. Ако сте забравили ODZ на логаритъм, силно препоръчвам да го повторите - вижте „Какво е логаритъм“.

Всичко, свързано с обхвата на допустимите стойности, трябва да бъде написано и решено отделно:

f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.

Тези четири неравенства съставляват система и трябва да бъдат изпълнени едновременно. Когато диапазонът от приемливи стойности е намерен, остава само да го пресечете с решението на рационалното неравенство - и отговорът е готов.

Задача. Решете неравенството:

Първо, нека напишем ODZ на логаритъма:

Първите две неравенства се изпълняват автоматично, но последното ще трябва да се изпише. Тъй като квадратът на число е нула тогава и само ако самото число е нула, имаме:

x 2 + 1 ≠ 1;
x2 ≠ 0;
x ≠ 0.

Оказва се, че ODZ на логаритъма са всички числа с изключение на нула: x ∈ (−∞ 0)∪(0; +∞). Сега решаваме основното неравенство:

Правим преход от логаритмично неравенство към рационално. Първоначалното неравенство има знак „по-малко от“, което означава, че полученото неравенство също трябва да има знак „по-малко от“. Ние имаме:

(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.

Нулите на този израз са: x = 3; x = −3; x = 0. Освен това x = 0 е корен от втора кратност, което означава, че при преминаване през него знакът на функцията не се променя. Ние имаме:

Получаваме x ∈ (−∞ −3)∪(3; +∞). Това множество се съдържа изцяло в ODZ на логаритъма, което означава, че това е отговорът.

Преобразуване на логаритмични неравенства

Често първоначалното неравенство е различно от горното. Това може лесно да се коригира с помощта на стандартните правила за работа с логаритми - вижте „Основни свойства на логаритмите“. а именно:

Всяко число може да бъде представено като логаритъм с дадена основа;
Сумата и разликата на логаритми с еднакви основи могат да бъдат заменени с един логаритъм.

Отделно бих искал да ви напомня за диапазона от допустими стойности. Тъй като в първоначалното неравенство може да има няколко логаритма, трябва да се намери VA на всеки от тях. По този начин общата схема за решаване на логаритмични неравенства е следната:

Намерете VA на всеки логаритъм, включен в неравенството;
Редуцирайте неравенството до стандартно, като използвате формулите за събиране и изваждане на логаритми;
Решете полученото неравенство, като използвате схемата, дадена по-горе.

Задача. Решете неравенството:

Нека намерим дефиниционната област (DO) на първия логаритъм:

Решаваме с помощта на интервалния метод. Намиране на нулите на числителя:

3x − 2 = 0;
х = 2/3.

След това - нулите на знаменателя:

x − 1 = 0;
х = 1.

Маркираме нули и знаци върху координатната стрелка:

Получаваме x ∈ (−∞ 2/3)∪(1; +∞). Вторият логаритъм ще има същия VA. Ако не вярвате, можете да проверите. Сега трансформираме втория логаритъм, така че основата да е две:

Както можете да видите, тройките в основата и пред логаритъма са намалени. Имаме два логаритма с една и съща основа. Нека ги съберем:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .

Получихме стандартното логаритмично неравенство. Отърваваме се от логаритмите с помощта на формулата. Тъй като първоначалното неравенство съдържа знак „по-малко от“, полученият рационален израз също трябва да бъде по-малък от нула. Ние имаме:

(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).

Имаме два комплекта:

ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
Отговорът на кандидата: x ∈ (−1; 3).

Остава да пресечем тези множества - получаваме истинския отговор:

Интересуваме се от пресечната точка на множества, така че избираме интервали, които са защриховани и на двете стрелки. Получаваме x ∈ (−1; 2/3)∪(1; 3) - всички точки са пробити.

Мислите ли, че има още време до Единния държавен изпит и ще имате време да се подготвите? Може би това е така. Но във всеки случай, колкото по-рано студентът започне подготовка, толкова по-успешно преминава изпитите. Днес решихме да посветим статия на логаритмичните неравенства. Това е една от задачите, което означава възможност за получаване на допълнителен кредит.

Знаете ли вече какво е логаритъм? Силно се надяваме. Но дори и да нямате отговор на този въпрос, това не е проблем. Разбирането какво е логаритъм е много просто.

Защо 4? Трябва да увеличите числото 3 до тази степен, за да получите 81. След като разберете принципа, можете да продължите към по-сложни изчисления.

Преминахте през неравенствата преди няколко години. И оттогава непрекъснато ги срещате в математиката. Ако имате проблеми с решаването на неравенства, вижте съответния раздел.
Сега, след като се запознахме с понятията поотделно, нека да преминем към тяхното разглеждане като цяло.

Най-простото логаритмично неравенство.

Най-простите логаритмични неравенства не се ограничават до този пример; има още три, само с различни знаци. Защо е необходимо това? За да разберете по-добре как да решавате неравенства с логаритми. Сега нека дадем по-приложим пример, все още доста прост;

Как да се реши това? Всичко започва с ODZ. Струва си да знаете повече за това, ако искате винаги лесно да решавате всяко неравенство.

Какво е ODZ? ОДЗ за логаритмични неравенства

Съкращението означава обхвата на допустимите стойности. Тази формулировка често се среща в задачите за Единния държавен изпит. ODZ ще ви бъде полезен не само в случай на логаритмични неравенства.

Погледнете отново горния пример. Ще разгледаме ODZ въз основа на него, за да разберете принципа и решаването на логаритмични неравенства не повдига въпроси. От дефиницията на логаритъм следва, че 2x+4 трябва да е по-голямо от нула. В нашия случай това означава следното.

Това число по дефиниция трябва да е положително. Решете представеното по-горе неравенство. Това може да се направи дори устно; тук е ясно, че X не може да бъде по-малко от 2. Решението на неравенството ще бъде дефинирането на диапазона от допустими стойности.
Сега нека преминем към решаването на най-простото логаритмично неравенство.

Изхвърляме самите логаритми от двете страни на неравенството. Какво ни остава в резултат? Просто неравенство.

Не е трудно да се реши. X трябва да е по-голямо от -0,5. Сега комбинираме двете получени стойности в система. По този начин,

Това ще бъде обхватът на приемливите стойности за разглежданото логаритмично неравенство.

Защо изобщо се нуждаем от ODZ? Това е възможност да отсеете грешните и невъзможни отговори. Ако отговорът не е в обхвата на приемливите стойности, тогава отговорът просто няма смисъл. Това си струва да се помни дълго време, тъй като в Единния държавен изпит често има нужда да се търси ODZ и това се отнася не само за логаритмични неравенства.

Алгоритъм за решаване на логаритмично неравенство

Решението се състои от няколко етапа. Първо, трябва да намерите диапазона от приемливи стойности. В ODZ ще има две значения, обсъдихме това по-горе. След това трябва да решите самото неравенство. Методите за решение са както следва:

метод за заместване на множителя;
разграждане;
метод на рационализация.

В зависимост от ситуацията си струва да използвате един от горните методи. Да преминем директно към решението. Нека разкрием най-популярния метод, който е подходящ за решаване на задачи от Единния държавен изпит в почти всички случаи. След това ще разгледаме метода на разлагане. Може да помогне, ако попаднете на особено сложно неравенство. И така, алгоритъм за решаване на логаритмично неравенство.

Примери за решения :

Не напразно взехме точно това неравенство! Обърнете внимание на основата. Запомнете: ако е по-голямо от едно, знакът остава същият при намиране на диапазона от допустими стойности; в противен случай трябва да промените знака за неравенство.

В резултат на това получаваме неравенството:

Сега намаляваме лявата страна до формата на уравнението, равно на нула. Вместо знака “по-малко” поставяме “равно” и решаваме уравнението. Така ще намерим ODZ. Надяваме се, че няма да имате проблеми с решаването на такова просто уравнение. Отговорите са -4 и -2. Това не е всичко Трябва да покажете тези точки на графиката, като поставите „+“ и „-“. Какво трябва да се направи за това? Заместете числата от интервалите в израза. Когато стойностите са положителни, поставяме „+“ там.

Отговор: x не може да бъде по-голямо от -4 и по-малко от -2.

Намерихме диапазона от приемливи стойности само за лявата страна; сега трябва да намерим диапазона от приемливи стойности за дясната страна. Това е много по-лесно. Отговор: -2. Пресичаме двете получени области.

И едва сега започваме да се занимаваме със самото неравенство.

Нека го опростим, доколкото е възможно, за да е по-лесно за решаване.

Отново използваме интервалния метод в решението. Нека пропуснем изчисленията, всичко вече е ясно от предишния пример. Отговор.

Но този метод е подходящ, ако логаритмичното неравенство има еднакви основи.

Решаването на логаритмични уравнения и неравенства с различни основи изисква първоначално редуциране до една и съща основа. След това използвайте метода, описан по-горе. Но има и по-сложен случай. Нека разгледаме един от най-сложните видове логаритмични неравенства.

Логаритмични неравенства с променлива основа

Как се решават неравенства с такива характеристики? Да, и такива хора могат да бъдат намерени в Единния държавен изпит. Решаването на неравенствата по следния начин също ще се отрази благотворно на учебния ви процес. Нека разгледаме въпроса в детайли. Да изоставим теорията и да преминем направо към практиката. За решаване на логаритмични неравенства е достатъчно да се запознаете с примера веднъж.

За да се реши логаритмично неравенство на представената форма, е необходимо да се намали дясната страна до логаритъм със същата основа. Принципът наподобява еквивалентни преходи. В резултат на това неравенството ще изглежда така.

Всъщност всичко, което остава, е да се създаде система от неравенства без логаритми. Използвайки метода на рационализация, преминаваме към еквивалентна система от неравенства. Ще разберете самото правило, когато замените подходящите стойности и проследите промените им. Системата ще има следните неравенства.

Когато използвате метода на рационализация при решаване на неравенства, трябва да запомните следното: едно трябва да се извади от основата, x, по дефиниция на логаритъма, се изважда от двете страни на неравенството (дясно от ляво), два израза се умножават и поставен под оригиналния знак по отношение на нула.

По-нататъшното решение се извършва с помощта на интервалния метод, тук всичко е просто. Важно е да разберете разликите в методите за решаване, тогава всичко ще започне да се получава лесно.

В логаритмичните неравенства има много нюанси. Най-простите от тях са доста лесни за решаване. Как можете да разрешите всеки от тях без проблеми? Вече сте получили всички отговори в тази статия. Сега ви предстои дълга практика. Постоянно практикувайте решаването на различни задачи на изпита и ще можете да получите най-висок резултат. Успех в нелеката задача!

Остава все по-малко време до преминаване на Единния държавен изпит по математика. Обстановката се нажежава, нервите на ученици, родители, учители и възпитатели стават все по-опънати. Ежедневните задълбочени занимания по математика ще ви помогнат да облекчите нервното напрежение. В края на краищата, както знаем, нищо не ви зарежда с позитивизъм и не ви помага да положите изпити, както увереността във вашите способности и знания. Днес учител по математика ще ви разкаже за решаването на системи от логаритмични и експоненциални неравенства, задачи, които традиционно създават трудности за много съвременни ученици.

За да научите как да решавате задачи С3 от Единния държавен изпит по математика като учител по математика, препоръчвам ви да обърнете внимание на следните важни точки.

1. Преди да започнете да решавате системи от логаритмични и експоненциални неравенства, трябва да научите как да решавате всеки от тези видове неравенства поотделно. По-специално, за да се разбере как се намира диапазонът от приемливи стойности, се извършват еквивалентни трансформации на логаритмични и експоненциални изрази. Можете да разберете някои от тайните, свързани с това, като изучавате статиите "" и "".

2. В същото време е необходимо да се разбере, че решаването на система от неравенства не винаги се свежда до решаване на всяко неравенство поотделно и пресичане на получените интервали. Понякога, знаейки решението на едно неравенство от системата, решението на второто става много по-просто. Като преподавател по математика, който подготвя учениците да се явят на финални изпити във формата на Единния държавен изпит, в тази статия ще разкрия няколко тайни, свързани с това.

3. Необходимо е ясно да се разбере разликата между пресичането и обединението на множества. Това е едно от най-важните математически знания, които опитен професионален учител се опитва да даде на своя ученик от първите уроци. Визуално представяне на пресичането и обединението на множества се дава от така наречените „окръжности на Ойлер“.

Пресечна точка на множества е множество, което съдържа само тези елементи, които има всяко от тези множества.

кръстовище

Представяне на пресечната точка на множества с помощта на „Ойлерови окръжности“

Обяснение на една ръка разстояние.Диана има „комплект“ в чантата си, състоящ се от ( химикалки, молив, владетели, тетрадки, гребени). Алис има „комплект“ в чантата си, състоящ се от ( тетрадка, молив, огледала, тетрадки, киевски котлети). Пресечната точка на тези две „множества“ ще бъде „множеството“, състоящо се от ( молив, тетрадки), тъй като и Даяна, и Алис имат и двата от тези „елементи“.

Важно е да запомните! Ако решението на неравенство е интервал и решението на неравенство е интервал, тогава решението на системите е:

е интервалът, който е кръстовище оригинални интервали. Тук и по-долуозначава някой от знаците title="Изобразено от QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">!} и под - това е обратният знак.

Обединение на комплекти е множество, което се състои от всички елементи на оригиналните множества.

С други думи, ако са дадени две групи и след това техните обединение ще бъде набор от следната форма:

Изобразяване на обединение на множество с помощта на „Ойлерови окръжности“

Обяснение на една ръка разстояние.Обединението на „множествата“, взети в предишния пример, ще бъде „множеството“, състоящо се от ( химикалки, молив, владетели, тетрадки, гребени, тетрадка, огледала, киевски котлети), тъй като се състои от всички елементи на оригиналните „набори“. Едно уточнение, което може би не е излишно. Няколко не могасъдържат идентични елементи.

Важно е да запомните! Ако решението на неравенство е интервал и решението на неравенство е интервал, тогава решението на съвкупността е:

е интервалът, който е съюз оригинални интервали.

Да преминем директно към примерите.

Пример 1.Решете системата от неравенства:

Решение на задача C3.

1. Нека решим първо първото неравенство. Използвайки заместването, отиваме до неравенството:

2. Нека решим второто неравенство. Диапазонът на неговите допустими стойности се определя от неравенството:

Title="Изобразено от QuickLaTeX.com">!}

В обхвата на приемливите стойности, като се има предвид, че основата на логаритъма title="Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству:!}

Като изключим решенията, които не са в обхвата на допустимите стойности, получаваме интервала

3. Отговаряте на системаще има неравенства кръстовище

Получените интервали на числовата ос. Решението е тяхното пресичане

Пример 2.Решете системата от неравенства:

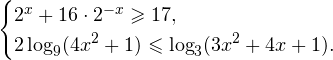
Решение на задача C3.

1. Нека решим първо първото неравенство. Умножете двете части по title="Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству:!}

Нека да преминем към обратното заместване:

Title="Изобразено от QuickLaTeX.com">!}

Графично представяне на получения интервал. Решението на системата е тяхното пресичане

Пример 3.Решете системата от неравенства:

Решение на задача C3.

1. Нека решим първо първото неравенство. Умножете двете части по title="Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство:!}

Използвайки заместване, стигаме до следното неравенство:

Нека да преминем към обратното заместване:

2. Нека решим второто неравенство. Нека първо определим обхвата на приемливите стойности на това неравенство:

ql-right-eqno">

Моля, имайте предвид, че

След това, като вземем предвид обхвата на приемливите стойности, получаваме:

3. Намираме общо решение на неравенствата. Сравняването на получените ирационални стойности на възловите точки в никакъв случай не е тривиална задача в този пример. Можете да направите това по следния начин. защото

Title="Изобразено от QuickLaTeX.com">!}

Че и крайният отговор на системата изглежда така:

Пример 4.Решете системата от неравенства:

Решение на задача C3.

1. Нека решим първо второто неравенство:

2. Първото неравенство от оригиналната система е логаритмично неравенство с променлива основа. Удобен начин за решаване на такива неравенства е описан в статията „Комплексни логаритмични неравенства“ и се основава на проста формула:

Всеки знак за неравенство може да бъде заменен със знака, основното е, че и в двата случая той е еднакъв. Използването на тази формула значително опростява решаването на неравенството:

Нека сега определим обхвата на приемливите стойности на това неравенство. Задава се по следната система:

Title="Изобразено от QuickLaTeX.com">!}

Лесно е да се види, че в същото време този интервал ще бъде и решение на нашето неравенство.

3. Окончателният отговор на оригинала системище има неравенства кръстовище получените интервали, т.е

Пример 5.Решете системата от неравенства:

Решение на задача C3.

1. Нека решим първо първото неравенство. Използваме заместване към следното квадратно неравенство:

2. Нека решим второто неравенство. Диапазонът на неговите допустими стойности се определя от системата:

Title="Изобразено от QuickLaTeX.com">!}

Това неравенство е еквивалентно на следната смесена система:

В обхвата на приемливите стойности, тоест с title="Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе:!}

Като вземем предвид диапазона от приемливи стойности, получаваме:

3. Окончателното решение на оригинала системие

Решение на задача C3.

1. Нека решим първо първото неравенство. Използвайки еквивалентни трансформации, го довеждаме до формата:

2. Нека решим второто неравенство. Диапазонът на неговите валидни стойности се определя от интервала: title="Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству:!}

Този отговор изцяло принадлежи към обхвата на приемливите стойности на неравенството.

3. Чрез пресичане на интервалите, получени в предходните параграфи, получаваме окончателния отговор на системата от неравенства:

Днес решавахме системи от логаритмични и експоненциални неравенства. Такива задачи бяха предложени в пробните варианти на Единния държавен изпит по математика през цялата учебна година. Въпреки това, като учител по математика с опит в подготовката за Единния държавен изпит, мога да кажа, че това изобщо не означава, че подобни задачи ще бъдат в реалните версии на Единния държавен изпит по математика през юни.

Позволете ми да отправя едно предупреждение, адресирано предимно до преподаватели и учители, които подготвят гимназисти за полагане на Единния държавен изпит по математика. Много е опасно да се подготвят ученици за изпит строго по зададени теми, тъй като в този случай съществува риск напълно да го „провалите“ дори с лека промяна в предварително заявения формат на задачите. Математическото образование трябва да е пълно. Уважаеми колеги, моля, не оприличавайте учениците си на роботи чрез така нареченото „обучение” за решаване на определен тип задачи. В крайна сметка няма нищо по-лошо от формализирането на човешкото мислене.

Успех и творчески успехи на всички!

Сергей Валериевич